Traitement des chiffres
Dans cette page, vous apprendrez à utiliser l'ordinateur pour faire des calculs. Vous utiliserez des instructions directes pour des calculs simples, ainsi que des programmes pour des calculs plus complexes. Vous utiliserez les opérateurs arithmétiques (+, -, *, /) et l'opérateur d'exponentiation (^) avec des nombres et des variables représentant des nombres. Vous en apprendrez plus sur :
- Comment utiliser les mots-clefs INPUT, LPRINT, LPRINT USING, PRINT USING et REM.
- Comment additionner, soustraire, multiplier et diviser en GW-BASIC.
- L'opérateur d'exponentiation et comment l'utiliser.
- Les différents types numériques, y compris les entiers, les nombres à simple précision et les nombres doubles.
- Notation à virgule flottante.
- Ce que sont les variables numériques et comment leur attribuer des valeurs.
- Comment utiliser l'instruction INPUT pour acquérir une valeur d'une variable.
- Comment utiliser les instructions PRINT USING et LPRINT USING pour afficher ou imprimer des nombres formatés et aligner les nombres verticalement.
Arithmétique avec instructions directes
Vous savez sûrement que l'ordinateur est comme une calculatrice. En GW-BASIC, vous pouvez utilisé les opérateurs arithmétiques +, -, * et / pour spécifier les opérations d'addition, de soustraction, de multiplication et de division afficher dans le tableau suivant :
| Opération | Symbole d'opération | Exemple |
|---|---|---|
| Addition | + | 3 + 4 |
| Soustraction | - | 3 - 4 |
| Multiplication | * | 3 * 4 |
| Division | / | 3 / 4 |
Pour demander à l'ordinateur d'effectuer des opérations arithmétiques, utilisez une instruction PRINT directe composée du mot-clef PRINT suivi d'une expression numérique (comme 3+4 ou 3-4). L'ordinateur évalue l'expression numérique (effectue l'arithmétique), puis affiche le résultat. Par exemple, demandez à l'ordinateur d'additionner les nombres 3 et 4, puis affiche le résultat.
Tapez :
| PRINT 3+4 |
Il affiche :
7Essayez maintenant les exemples suivants. Appuyez sur ENTER après avoir tapé une instruction PRINT directe. N'oubliez pas que vous pouvez utiliser ALT+P comme raccourci pour PRINT. Vous pouvez également utiliser un point d'interrogation (?) comme abréviation pour PRINT, comme indiqué ici :
Type :
Tapez :
| ? 3+4 |
Il affiche :
-1Marise mesure 1,50 m. Convertissez sa taille en centimètres. Un pouce équivaut à 2,54 centimètres.
Type :
| PRINT 59*2.54 |
Il affichera :
-1Un ancien souverain nommé Manic mesurait 100 centimètres du bout de son nez jusqu'au bout de ses bras tendus. Quelle est cette longueur en pouces ?
| PRINT 100 / 2.54 |
Il affichera :
39.37008Ce nombre vous semble familier ? Vous vous souvenez peut-être que 100 centimètres équivalent à un mètre. Un mètre équivaut à 39,37 pouces, soit un peu plus d'un yard.
Les gens donnent généralement leur taille en pieds et en pouces. Si vous demandez à Marise quelle est sa taille, elle vous dira probablement qu'elle mesure 4 pieds et 11 pouces. Il est facile d'écrire une instruction PRINT pour convertir les pieds et les pouces en pouces.
Tapez :
| PRINT 4 * 12 + 11 |
Il affichera :
59L'ordinateur effectue d'abord la multiplication (4 fois 12), puis l'addition (plus 11). Pour évaluer une expression, l'ordinateur effectue d'abord les multiplications et les divisions, puis les additions et les soustractions.
Presque tout le monde reçoit une facture mensuelle d'une compagnie d'électricité. Le gaz est mesuré en thermes et l'électricité en kilowattheures (kWh). Calculez le montant d'une facture mensuelle pour 53 thermes de gaz à 0,41 $ et 295 kWh d'électricité à 0,08 $.
Tapez :
| PRINT 53 * .41 + 295 * 0.8 |
Il affichera :
45.33Pour évaluer cette expression, l'ordinateur effectue les deux multiplications, puis additionne les deux résultats pour obtenir le résultat final.
Avant d'atteindre sa taille adulte, King Kong mesurait 11,32 mètres. Quelle était sa taille en centimètres ?
Tapez :
| PRINT (37 * 12 + 9) * 2.54 |
Il affichera :
1150.62Notez l'utilisation des parenthèses. L'ordinateur effectue d'abord les opérations arithmétiques à l'intérieur des parenthèses, puis fait le reste. L'exemple 6 utilise également des parenthèses.
Au début d'un trajet en voiture, le compteur kilométrique affichait 19 832 miles. À la fin du trajet, il affichait 20 219 miles. La voiture a consommé 9,3 gallons d'essence. Combien de kilomètres par gallon la voiture a-t-elle parcourus pendant ce trajet ?
Tapez :
| PRINT (20219-19832) / 9.3 |
Il affichera :
41.6129Notez que les virgules n'ont pas été utilisées lors de la saisie des nombres 20219 et 19832. Les virgules ne peuvent pas être utilisées dans un nombre, bien que les virgules (et les points-virgules) puissent être utilisées pour séparer les expressions numériques dans les commandes PRINT.
Exposants et nombres à virgule flottante
Vous avez utilisé les opérateurs arithmétiques (+, -, *, /) pour additionner, soustraire, multiplier et diviser des nombres. Vous allez maintenant utiliser un autre opérateur, l'opérateur d'exponentiation (^), pour calculer une puissance d'un nombre.
L'opérateur d'exponentiation (^)
Une pièce dans une maison a un sol de 12 pieds carrés. Autrement dit, le sol est carré et chaque côté du carré mesure 12 pieds de long. Quelle est l'aire de la pièce en pieds carrés ? Voici deux façons de calculer l'aire.
La première méthode utilise la multiplication.
Tapez :
| PRINT 12 * 12 |
Il affichera :
144La deuxième méthode utilise l'opérateur d'exponentiation (^) pour calculer le carré de 12, également appelé la seconde puissance de 12. Pour saisir le symbole d'exponentiation (^), maintenez la touche SHIFT enfoncée et appuyez sur la touche comportant à la fois le chiffre 6 et le symbole d'exponentiation (^).
Tapez :
| PRINT 12 ^ 2 |
Il affichera :
144Supposons maintenant que la pièce ait un plafond assez haut, exactement 12 pieds de haut. Quelle coïncidence fortuite ! La pièce mesure 12 par 12 par 12. Par conséquent, le volume de la pièce est 12 fois 12 fois 12, soit 12 au cube. Une autre façon de dire «12 au cube» est 12 à la troisième puissance, ou «la troisième puissance de 12». Vous pouvez calculer le volume en pieds cubes de deux manières.
Utilisez la multiplication (*).
Tapez :
| PRINT 12 * 12 * 12 |
Il affichera :
1728Ou utilisez l'exponentiation (^).
Tapez :
| PRINT 12 ^ 3 |
Il affichera :
1728Dans les manuels de mathématiques, les carrés et les cubes des nombres sont indiqués au moyen de nombres en exposant. Les nombres 12 au carré et 12 au cube sont indiqués ci-dessous à la fois en notation mathématique standard et en notation GW-BASIC.
| Notation mathématique | Notation GW-BASIC | Signification |
|---|---|---|
| 122 | 12^2 | 12 au carré, ou 12 à la deuxième puissance |
| 123 | 12^3 | 12 au cube, ou 12 à la troisième puissance |
Dans une expression telle que 12^3, le nombre 12 est la base et 3 est l'exposant. L'exposant indique combien de fois la base doit être utilisée comme facteur. Voici quelques exemples.
| Expression | Base | Exposant | Équivalent par multiplication |
|---|---|---|---|
| 12^2 | 12 | 2 | 12*12 |
| 12^3 | 2 | 3 | 12*12*12 |
| 5^4 | 5 | 4 | 5*5*5*5 |
| 2^10 | 2 | 10 | 2*2*2*2*2*2*2*2*2*2 |
Les exposants peuvent être très utiles. Il est beaucoup plus facile d'écrire 2^10 (2 à la puissance 10) que d'écrire 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2. Considérez également l'expression des capacités de mémoire d'un ordinateur. Les gens disent qu'un ordinateur a 256 Ko, 512 Ko, 640 Ko ou plus d'octets de mémoire. K est une abréviation du terme métrique kilo, signifiant 1 000. Un kilogramme équivaut à 1 000 grammes ; un kilomètre équivaut à 1 000 mètres. Cependant, 1 K octets équivaut en réalité à 2^10 octets. Les exemples suivants utilisent l'opérateur d'exponentiation (^) pour calculer le nombre d'octets dans 1 K, 512 K et 640 K.
Tapez :
| PRINT 2^10 |
Il affichera :
1024Tapez :
| PRINT 512*2^10 |
Il affichera :
524288Tapez :
| PRINT 640*2^10 |
Il affichera :
655360Pour évaluer l'expression 512*12^10, l'ordinateur calcule d'abord la puissance dixième de 2 (2^10), puis multiplie ce résultat par 512.
Nombre à virgule flottante
Les mémoires informatiques sont de plus en plus grandes. Les mémoires d'un, deux ou plusieurs mégaoctets sont de plus en plus courantes. Le terme «méga» est également emprunté au système métrique. Dans le système métrique, il signifie un million. Cependant, en référence à la taille des mémoires d'ordinateur ou à la capacité d'entreposage du disque dur, il signifie 2^20 (2 à la puissance vingtième, ou la puissance vingtième de 2).
Combien d'octets dans un mégaoctet ? Utilisez GW-BASIC pour le savoir.
Tapez :
| PRINT 640*2^10 |
Il affichera :
1048576Un mégaoctet équivaut à 1 048 576 octets, et non à 1 000 000 octets. Ensuite, calculez le nombre d'octets dans un disque dur de 20 mégaoctets.
Tapez :
| PRINT 20*2^20 |
Il affichera :
2.09752E+07Vingt mégaoctets équivalent à 20 fois 1 mégaoctet, donc 20 mégaoctets équivalent à 20 fois 2^20.
GW-BASIC affiche ce grand nombre sous forme de nombre à virgule flottante. Lisez-le ainsi : 2,097152E+07 est 2,097152 fois 10^7 (10 à la puissance sept). La notation à virgule flottante est très similaire à la notation scientifique, utilisée dans les livres de mathématiques et de sciences, comme illustré ici :
| Description | Exemple |
|---|---|
| Notation à virgule flottante : | 2.097152E+07 |
| Notation scientifique : | 2,097152x107 |
La notation à virgule flottante est simplement une manière abrégée d'exprimer de grands nombres. Un nombre à virgule flottante est composé de deux parties : une mantisse et un exposant. La mantisse et l'exposant sont séparés par la lettre E (pour exposant), comme indiqué ici :
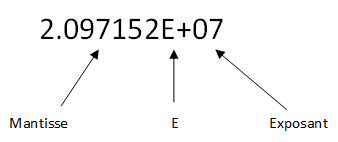
Dans un nombre à virgule flottante, l'exposant est toujours une puissance de 10. Voici d'autres exemples de grands nombres affichés en notation «ordinaire», en notation à virgule flottante et en notation scientifique.
| Nombre | Notation ordinaire | Virgule flottante | Scientifique |
|---|---|---|---|
| Population de la Terre | 8000000000 | 8E+09 | 8x109 |
| Trois mille milliards | 3000000000000 | 3E+12 | 3x1012 |
| Des kilomètres en une année-lumière | 5865696000000 | 5.865696E+12 | 5.865696x1012 |
La dette nationale des États-Unis s'élève à environ trois mille milliards de dollars et la population est d'environ 250 millions d'habitants. Vous pouvez utiliser des nombres flottants pour calculer la dette de chaque personne, comme le montre l'exemple suivant :
Tapez :
| PRINT 3E12 / 250E6 |
Il affichera :
12000La dette de chaque personne dans le pays est de 12 000 $ ! Trois mille milliards sont égaux à 3 fois 10^12. En notation à virgule flottante, cela donne 3E+12. Deux cent cinquante millions sont égaux à 250 fois 10^6. En notation à virgule flottante, cela donne 250E+6. Notez que vous pouvez écrire trois mille milliards sous la forme 3E12 au lieu de 3E+12. De plus, 250 millions peuvent être écrits sous la forme 250E6 au lieu de 250E+06, ou 2,5E+08 ; les trois manières sont acceptables.
Les petits nombres
Comme vous l'avez vu, GW-BASIC fait du bon travail en représentant des nombres plus grands au moyen de la notation à virgule flottante. Il est également capable de représenter de très petits nombres.
Une expérience récente a déterminé qu'un escargot effrayé se déplace à la vitesse d'un pouce toutes les quatre secondes. Quelle est cette vitesse en miles par seconde ? Voyons maintenant, l'escargot se déplace à 0,25 pouce par seconde. Divisez ce nombre par le nombre de pouces dans un mile. Il y a 5280 pieds dans un mile, donc calculez d'abord le nombre de pouces, comme suit :
Type :
| PRINT 12 * 5280 |
Il affichera :
63360Divisez maintenant la vitesse de l'escargot en pouces par seconde par 63 360.
Tapez :
| PRINT 0.25 / 63360 |
Il affichera :
3.945707E-06GW-BASIC affiche ce très petit nombre sous forme de nombre à virgule flottante avec une mantisse (3,945707) et un exposant négatif (-06). La mantisse et l'exposant sont séparés par la lettre E. Lisez-le ainsi : trois virgule neuf quatre cinq sept zéro sept fois dix puissance moins 6. Dans les livres de mathématiques, de sciences ou autres ouvrages de haute technologie, vous pouvez voir ce nombre écrit en notation scientifique sous la forme 3,945707x10-6.
| Description | Exemple |
|---|---|
| Notation à virgule flottante : | 3.945707E-06 |
| Notation scientifique : | 3,945707x10-6 |
L'hydrogène est une substance universelle. Il a commencé avec le Big Bang ayant créé l'univers. Il est présent ici, là, partout. L'atome d'hydrogène est très petit et léger. Sa masse est d'environ 1,67 x 10 kilogrammes.
| Description | Exemple |
|---|---|
| Notation à virgule flottante : | 1.67E-27 |
| Notation scientifique : | 1,67x10-27 |
| Notation ordinaire : | .000000000000000000000000000167 |
Comme vous pouvez le voir, vous pouvez taper le nombre beaucoup plus rapidement en virgule flottante qu'en notation ordinaire, et avec moins de risques d'erreur de frappe.
Types de nombres
Le GW-BASIC possède plusieurs types de nombres : les entiers, les nombres à simple précision, les nombres à double précision et les nombres à virgule flottante. Jusqu'à présent, vous avez vu trois types : les entiers, les nombres à simple précision et les nombres à virgule flottante, dont des exemples sont présentés ici :
| Description | Exemple |
|---|---|
| Entiers : | 3 4 -1 12 |
| Nombres à simple précision : | 2.54 1148.08 655360 |
| Nombres à virgule flottante : | 2.097152E+07 3E12 250E6 |
Un entier est un nombre entier (c'est-à-dire un nombre sans décimale) compris entre -32 768 et 32 767. Un entier est entreposé dans deux octets de mémoire. Un nombre à simple précision peut être un entier ou un non-entier ou un non-entier comportant jusqu'à sept chiffres. Un nombre à simple précision est entreposé dans quatre octets de mémoire.
Un nombre à virgule flottante est un nombre avec une mantisse et un exposant. La mantisse peut comporter jusqu'à sept chiffres. L'exposant est compris entre -39 et +38. Un nombre à virgule flottante est entreposé dans quatre octets de mémoire.
Explorez maintenant un modèle de nombre. Effacez l'écran et procédez comme suit :
| Exemple | Résultat |
|---|---|
| PRINT 11 * 11 | 121 |
| PRINT 111 * 111 | 12321 |
| PRINT 1111 * 1111 | 1234321 |
| PRINT 11111 * 1111 | 1.234543E+07 |
Les deux premiers résultats (121 et 12321) peuvent être considérés comme des entiers ou des nombres à simple précision. Le troisième résultat (1234321) est un nombre à simple précision. Le cinquième résultat (1,234543E+07) est un nombre à virgule flottante. Cependant, il ne s'agit pas de la réponse exacte, étant 123454321. Il s'agit plutôt d'une approximation à sept chiffres du résultat. Heureusement, il existe un autre type de nombre que vous pouvez utiliser pour représenter correctement les nombres à plus de sept chiffres.
Nombres à double précision
Un nombre à double précision peut comporter jusqu'à 16 chiffres. Vous pouvez spécifier un nombre en double précision en lui ajoutant un symbole numérique (#).
Tapez :
| PRINT 11111 * 11111# |
Il affichera :
123454321Le nombre 11111# est un nombre à double précision. Par conséquent, l'expression 11111 * 11111# est évaluée comme un résultat à double précision et la réponse (123454321) est affichée correctement. Vous pouvez également écrire l'expression de la manière suivante :
Tapez :
| PRINT 11111# * 11111 |
Il affichera :
123454321Si un opérande dans une expression est en double précision, l'ordinateur traite l'expression entière comme une expression en double précision.
Maintenant, continuons le modèle.
Tapez :
| PRINT 111111 * 111111# |
Il affichera :
12345654321Si vous continuez, vous verrez bientôt un nombre à virgule flottante à double précision, comme illustré ici :
Tapez :
| PRINT 11111111 * 11111111# |
Il affichera :
1.234567898765432D+16Un nombre à virgule flottante à double précision se compose d'une mantisse et d'un exposant séparés par la lettre D. La mantisse peut comporter jusqu'à 16 chiffres. L'exposant a la même plage que les nombres à simple précision, de -39 à +38. Un nombre à double précision est entreposé dans huit octets de mémoire.
N'oubliez pas : les entiers sont des nombres entiers (sans point décimal) compris entre -32768 et 32767. Un entier est entreposé dans deux octets de mémoire. Les nombres à simple précision sont des nombres réels (entiers ou non entiers) comportant jusqu'à sept chiffres et, éventuellement, un point décimal. Un nombre à simple précision peut apparaître comme un nombre à virgule flottante composé d'une mantisse, de la lettre E et d'un exposant. Un nombre à double précision est un nombre réel (entier ou non entier) comportant jusqu'à 16 chiffres et un point décimal. Un nombre à double précision peut apparaître comme un nombre à virgule flottante à double précision composé d'une mantisse, de la lettre D et d'un exposant.
Variables numériques
Imaginez que, dans la mémoire de l'ordinateur, il existe de nombreuses «cases numériques». Chaque case numérique peut contenir un nombre à la fois. Un nombre de boites peut contenir, ou entreposer, différents nombres à différents moments. L'illustration suivante contient des cases numériques appelées a, diametre et prix. Chaque case numérique contient un nombre.

Le numéro 7 se trouve dans la case numérique a ; 24 se trouve dans la case numérique appelée diametre ; la case numérique intitulée prix contient le numéro 19,95.
Dans GW-BASIC, une case numérique est appelée une variable numérique. Le nombre dans une case numérique est la valeur de la variable identifiant la case. Par conséquent :
- La valeur de la variable a est 7 ;
- La valeur de la variable diametre est 24.
- La valeur de la variable prix est 19,95.
Vous pouvez créer des noms de variables, sous réserve des limitations suivantes :
- Un nom de variable peut être une simple lettre ou toute combinaison de lettres et de chiffres (0 à 9) d'une longueur maximale de 40 caractères.
- Le premier caractère doit être une lettre.
- Vous ne pouvez pas utiliser un mot clef GW-BASIC (tel que BEEP, CLS ou PRINT) comme variable, mais un mot clef peut faire partie d'une variable. Par exemple, «beeper» est correct même s'il contient «beep».
Voici sept exemples de noms de variables :
- a diametre prix pi Qty R2D2 TaxRate
Notez que les lettres peuvent être en majuscules (A, B, C...) ou en minuscules (a, b, c,...). Le GW-BASIC ne fait pas de distinction entre les majuscules et les minuscules. Par conséquent, a et A sont la même variable, pi et PI sont la même variable ; taxRate et TaxRate sont la même variable. Néanmoins, dans cette page, les noms de variables apparaissent en minuscules, ou un mélange de minuscules et de majuscules. Cela permet de distinguer facilement les variables des mots-clefs (BEEP, CLS, PRINT, ...), apparaissant toujours en majuscules.
Types de variables numériques
Étant donné que GW-BASIC possède trois types de nombres, il possède également trois types de variables : les variables entières, les variables à simple précision et les variables à double précision. Une variable entière ne peut avoir que des valeurs entières. Une variable à simple précision peut avoir des nombres à simple précision comme valeurs. Une variable à double précision peut avoir des nombres à double précision comme valeurs.
Une variable entière se compose d'un nom de variable suivi d'un signe de pourcentage (%). Le signe de pourcentage désigne la variable comme une variable entière.
- Variables entières : n% Qty% Year%
Une variable à double précision se compose d'un nom de variable suivi d'un symbole numérique (#).
- Variables à double précision : BigNumber# DollarsdeLostsa DetteNationale#
Une variable de précision simple se compose d'un nom de variable suivi d'aucun désignateur ou d'un point d'exclamation (!).
- Variables de précision simple : x Prix Prix! pi pi!
N'oubliez pas : un nom de variable sans désignateur (%, ! ou #) est automatiquement une variable à simple précision. Les variables à simple précision suffisent pour la plupart des programmes. D'autres variables sont utilisées si nécessaire. Par exemple, les variables à double précision sont nécessaires pour les problèmes impliquant de grosses sommes d'argent.
Affecter une valeur à une variable numérique
Vous pouvez utiliser des instructions directes pour affecter une valeur à une variable, puis imprimer la valeur de la variable. Faites-le maintenant. Effacez l'écran et affectez la valeur 7 à la variable a.
Tapez :
| a = 7 |
et appuyez sur ENTER.
Vous verrez ce qui suit à l'écran :
|
a = 7 Ok _ |
GW-BASIC a maintenant réservé une petite partie de la mémoire (quatre octets) comme variable de précision simple nommée a, et a attribué le nombre 7 comme valeur de a. Lorsque vous tapez a = 7 et appuyez sur ENTER, vous dites à l'ordinateur d'attribuer la valeur 7 à la variable nommée a.
Utilisez maintenant une instruction PRINT directe pour dire à l'ordinateur d'afficher la valeur de a.
Tapez :
| PRINT a |
Il affichera :
7La valeur d'une variable reste la même jusqu'à ce que vous la modifiiez. Vous pouvez le vérifier en répétant l'instruction précédente.
Tapez :
| PRINT a |
Il affichera :
7L'ordinateur a de nouveau affiché la valeur de a, étant 7.
Maintenant, attribuez un autre numéro à la valeur de a, puis affichez-le. Votre nouveau numéro remplacera l'ancienne valeur a.
Tapez :
| A = 1.23 |
Tapez ensuite :
| PRINT a |
Il affichera :
1.23Affectez la valeur 3,14 à une nouvelle variable, pi, et affichez la valeur de pi.
Tapez :
| pi = 3.14 |
Tapez ensuite :
| PRINT pi |
Il affichera :
3.14pi et a conservent leurs valeurs jusqu'à ce qu'elles soient modifiées. Confirmez cela en affichant les deux variables. Vous pouvez le faire avec une seule instruction PRINT, en utilisant une virgule (,) entre les deux variables.
Tapez :
| PRINT pi,a |
Il affichera :
3.14 1.23Vous pouvez utiliser des variables dans des expressions arithmétiques. Affectez des valeurs aux variables a et b, comme indiqué ici :
Tapez :
| a = 7 |
Tapez ensuite :
| b = 5 |
Utilisez maintenant les variables a et b dans les instructions PRINT pour effectuer des opérations arithmétiques.
Tapez :
| PRINT a + b |
Il affichera :
12Tapez :
| PRINT a - b |
Il affichera :
2Tapez :
| PRINT a * b |
Il affichera :
35Tapez :
| PRINT a / b |
Il affichera :
1.4Deux vélos ont des roues de 21 et 24 pouces de diamètre. Quelle distance parcourt chaque vélo en un tour de roue ? La distance est le diamètre multiplié par pi (π), où pi est approximativement égal à 3,14. Tout d'abord, attribuez la valeur 3,14 à pi.
Tapez :
| pi = 3.14 |
Utilisez maintenant Pi pour calculer la distance parcourue par chaque vélo en un tour de roue.
| Vélo #1 | Vélo #2 | |||
|---|---|---|---|---|
|
Tapez :
Il affichera : 65.94 |
Tapez :
Il affichera : 75.36 |
Les réponses dans les exemples précédents sont en pouces. Si vous voulez les résultats en pieds, procédez ainsi :
| Vélo #1 | Vélo #2 | |||
|---|---|---|---|---|
|
Tapez :
Il affichera : 5.495001 |
Tapez :
Il affichera : 6.28 |
Le taux de taxe de vente locale est de 6 %. Affectez cette valeur à la variable TaxRate, comme suit :
Tapez :
| TaxRate = .06 |
La valeur de TaxRate est de 0,06, puisque 6 % correspondent à 6/100, ou 0,06 lorsqu'elle est exprimée sous forme décimale. Vous pouvez également attribuer la valeur de TaxRate comme indiqué ici :
| TaxRate = 6 / 100 |
Vous pouvez désormais utiliser TaxRate pour calculer le montant de la taxe de vente pour différentes sommes d'argent. Voici deux exemples.
Vous achetez un article coûtant 169 $. Quel montant de taxe de vente allez-vous payer sur cet achat ?
Tapez :
également attribuer la valeur de TaxRate comme indiqué ici :| PRINT 169 * TaxRate |
Il affichera :
10.14Vous achetez un jeu informatique coûtant 29,95 $. À combien s'élève la taxe de vente ?
Tapez :
| PRINT 29.95 * TaxRate |
Il affichera :
1.797Arrondie au centime le plus proche, la taxe sur le jeu informatique à 29,95 $ est de 1,80 $. Plus loin dans cette page, vous apprendrez comment afficher des résultats arrondis au centime le plus proche.
Programmation avec des variables
L'ordinateur devient un outil beaucoup plus puissant et utile si vous créez des programmes effectuant des calculs à l'aide de variables. Les valeurs des variables peuvent être saisies selon les besoins à partir du clavier. Le programme peut alors effectuer la plupart du travail automatiquement.
L'instruction INPUT
L'instruction INPUT permet de saisir les valeurs des variables selon les besoins d'un programme. Dans sa forme la plus simple, une instruction INPUT se compose du mot clef INPUT suivi d'une variable.
Le programme suivant (Taxe de vente avec instruction INPUT) illustre l'utilisation d'une instruction INPUT pour acquérir la valeur de la variable SalesAmount :
Entrez ce programme dans la mémoire de l'ordinateur, comme suit :
- Tout d'abord, tapez NEW et appuyez sur ENTER. Cela efface la partie de la mémoire utilisée pour les programmes GW-BASIC. L'ordinateur est prêt pour un nouveau programme.
- Tapez chaque ligne du programme et appuyez sur ENTER. Vous pouvez utiliser ALT+P comme raccourci pour taper PRINT ; vous pouvez également utiliser ALT+I comme raccourci pour taper INPUT.
Après avoir saisi le programme, listez-le à l'écran.
N'oubliez pas : pour lister un programme, vous pouvez taper LIST et appuyer sur ENTER. Vous pouvez également utiliser un raccourci ; appuyez sur la touche de fonction F1, puis appuyez sur ENTER. Le programme doit apparaître comme indiqué ici :
|
LIST 10 CLS 20 TaxRate = 6 / 100 30 INPUT SalesAmount 40 PRINT SalesAmount * TaxRate Ok _ |
Comme vous pouvez le constater dans la liste du programme, GW-BASIC convertit les noms de variables en lettres majuscules, quelle que soit la manière dont ils ont été saisis. Si vous saisissez des mots-clefs en minuscules, ils sont également convertis en majuscules. Néanmoins, dans cette page, les variables sont affichées soit en minuscules, soit en un mélange de majuscules et de minuscules, sauf dans les listes. Cela a pour but de rendre les programmes plus faciles à lire.
Maintenant, la touche de fonction F2. En appuyant sur F2, le programme exécute immédiatement ; vous n'avez même pas besoin d'appuyer sur ENTER.
Le programme efface d'abord l'écran (ligne 10), puis définit la valeur de TaxRate à 0,06 (ligne 20) ; puis exécute l'instruction INPUT à la ligne 30. Il affiche un point d'interrogation sur l'écran, active le curseur clignotant et attend. Le haut de l'écran ressemble à ceci :
| ? _ |
L'ordinateur attend que vous saisissiez une valeur de SalesAmount et que vous appuyiez sur ENTER. Si vous saisissez 169 et appuyez sur ENTER, l'ordinateur acceptera ce nombre comme valeur de SalesAmount, calculera et affichera la taxe de vente (ligne 40) et s'arrêtera, comme indiqué ici :
|
? 169 1.14 Ok _ |
Exécutez à nouveau le programme (appuyez sur F2). Cette fois, entrez 29.95 comme valeur de SalesAmount :
|
? 29.95 1.797 Ok _ |
Exécutez à nouveau le programme et saisissez le numéro de votre choix. Essayez également de saisir des nombres tels que 1, 10 ou 100, afin de pouvoir facilement vérifier que le programme fonctionne correctement et produit les bonnes réponses. Examinez ensuite le programme ; il fonctionne comme décrit dans le tableau suivant :
| Ligne de programme | Explication |
|---|---|
| 10 CLS | Effacer l'écran |
| 20 TaxRate = 6 / 100 | Divise 6 par 100 et attribuez le résultat comme valeur de TaxRate. |
| 30 INPUT SalesAmount | Affiche un point d'interrogation et attendez qu'un numéro soit saisi. |
| 40 PRINT SalesAmount * TaxRate | Calcule le montant de la taxe de vente et l'affiche. |
Si le taux de taxe de vente dans votre quartier est différent de 6 %, modifiez la ligne 20 du programme. Par exemple, si le taux de taxe est de 6,5 %, remplacez la ligne 20 actuelle comme suit :
Tapez :
- 20 TaxRate = 6.5 / 100
Répertoriez le programme pour vérifier que la modification a été effectuée correctement, puis exécutez le programme modifié.
N'oubliez pas : pour remplacer une ligne d'un programme, tapez la nouvelle ligne en utilisant le numéro de la ligne que vous souhaitez remplacer. Vous pouvez également modifier une ligne en la listant à l'écran, en modifiant la ligne et en appuyant sur ENTER. Pour lister uniquement la ligne 20, tapez LIST 20 et appuyez sur ENTER.
Sauvgarde le programme
Enregistrez le programme GWSM0002 sur l'unité de disque par défaut. La manière la plus simple de procéder est la suivante :
- Appuyez sur la touche de fonction F4.
- Tapez le nom du fichier (GWSM0001).
- Appuyez sur ENTER.
C'est aussi simple que 1-2-3. L'instruction SAVE apparaîtra comme indiqué ici :
| SAVE"GWSM0001 |
Notez que les guillemets fermants ne sont pas obligatoires, sauf si vous souhaitez enregistrer le programme sous forme de fichier texte ASCII. Dans ce cas, tapez l'instruction SAVE de cette façon :
| SAVE"GWSM0001",A |
Si vous souhaitez enregistrer le programme sur un unité de disque désigné, incluez la lettre du pilote suivie de deux points (:) dans le nom de fichier, comme indiqué ici pour l'unité de disque B :
| SAVE"B:GWSM0001 | SAVE"B:GWSM0001",A |
Après avoir enregistré le programme, utilisez une instruction FILES pour vérifier que le programme se trouve sur le disque. Deux exemples d'instructions FILES sont présentés ci-dessous : l'une pour examiner le lecteur de disque par défaut et l'autre pour vérifier que les fichiers se trouvent sur l'unité de disque B.
- Pour voir l'unité de disque par défaut : FILES
- Pour voir l'unité de disque B : FILES "B"
Remarques sur le programme
Il est bon de placer des informations au début d'un programme pour informer les utilisateurs sur le programme. L'instruction REM (REMark) vous permet de le faire. Tout texte suivant REM dans une ligne de programme est ignoré lorsque vous exécutez le programme. Vous pouvez utiliser une apostrophe (') comme abréviation pour REM.
Ajoutons quatre lignes REM au programme GWSM0001. Si le programme n'est pas actuellement en mémoire, utilisez d'abord l'une des instructions LOAD suivantes pour le charger du disque vers la mémoire :
- Pour charger à partir du lecteur de disque par défaut : LOAD "GWSM0001"
- Pour charger à partir du lecteur de disque B : LOAD "B:GWSM0001"
N'oubliez pas : vous pouvez appuyer sur F3 pour saisir LOAD". Ajoutez maintenant les quatre lignes indiquées ici. Tapez simplement chaque ligne et appuyez sur ENTER :
- 1 REM ** Taxe de vente avec instruction INPUT **
- 2 ' GW-BASIC, fichier : GWSM0001
- 3 ' Écrit un jour pluvieux de janvier
- 9 '
Répertoriez le programme. Vous devriez voir le programme d'origine, plus les quatre lignes ci-dessus, le tout dans l'ordre des numéros de ligne, comme indiqué ici :
|
LIST 1 REM ** Taxe de vente avec instruction INPUT ** 2 ' GW-BASIC, fichier : GWSM0001 3 ' Écrit un jour pluvieux de janvier 9 ' 10 CLS 20 TaxRate = 6 / 100 30 INPUT SalesAmount 40 PRINT SalesAmount * TaxRate |
La ligne 1 est une instruction REM décrivant brièvement le programme. La ligne 2 utilise une apostrophe (') au lieu du mot REM. Elle indique l'origine du programme et donne le nom de fichier (GWSM0001) sous lequel il est stocké sur un disque. Le nom de fichier complet, y compris l'extension .BAS, est affiché, la ligne 3 est facultative. Vous pouvez mettre les commentaires que vous voulez dans ces premières lignes. Vous pouvez inclure la date à laquelle le programme a été écrit ou la date de la dernière modification du programme. La ligne 9 sert d'espaceur de ligne vide, séparant ce bloc d'informations descriptives du reste du programme, qui fait le travail réel. Vous pouvez mettre cinq lignes supplémentaires (4, 5, 6, 7 et 8) entre la ligne 3 et la ligne 9.
Les informations contenues dans les instructions REM sont destinées aux personnes ; l'ordinateur les ignore. Exécutez le programme pour vérifier cela. À partir de maintenant, la plupart des programmes auront des instructions REM vous aidant à identifier et à comprendre les programmes.
Un programme de taxe de vente amélioré
L'instruction INPUT demande à l'ordinateur de placer un point d'interrogation sur l'écran et d'attendre qu'un nombre soit saisi. Cela est utile, mais ce serait encore plus utile si l'ordinateur identifiait le type de saisie qu'il souhaite. Il existe un moyen simple de le faire.
Le programme GWSM0002 (Taxes de vente avec instruction INPUT améliorée) est une version améliorée du programme de taxe de vente. Il comporte une instruction INPUT « améliorée ».
Première exécution
|
Montant de la vente ? 169 10.14 Ok _ |
Deuxième exécution
|
Montant de la vente ? 29.95 10.14 Ok _ |
Exécutez le programme. Deux exemples d'exécution sont présentés ici :
L'instruction :
| INPUT "Montant de la vente";SalesAmount |
indique à l'ordinateur de faire ce qui suit :
- Affichez le message «Montant de la vente».
- Affichez un point d'interrogation.
- Attendez qu'un nombre soit saisi et attribuez-le comme valeur de SalesAmount.
Notez que le message à afficher est placé entre guillemets et suivi d'un point-virgule.
Modifiez maintenant le programme afin qu'il identifie le résultat comme le montant de la taxe de vente, comme indiqué dans le programme GWSM0003. Assurez-vous de saisir tous les signes de ponctuation, y compris les guillemets ("").
Enregistrez le programme sous le nom de fichier GWSM0003, puis exécutez-le. Un exemple d'exécution est présenté ici :
|
Montant de la vente ? 29.95 Le montant de la vente avec taxe est : 1.797 Ok _ |
Formatage des résultats affichés
La prochaine version du programme de taxe de vente GWSM0004 est considérablement étendue. Elle imprime le montant de la vente saisi au clavier, le montant de la taxe de vente et le montant total de la vente, taxe de vente comprise. La fonction TAB est utilisée pour aligner les chiffres verticalement. Des lignes vides sont ajoutées pour faciliter la lecture du programme. Ces lignes vides n'apparaîtront pas lorsque vous listerez le programme.
Notez plusieurs nouveautés dans ce programme :
- 1 REM ** Taxe de vente étendu **
- 2 ' GW-BASIC, fichier : GWSM0004
-
- 10 CLS
- 20 TaxRate = 6 / 100
-
- 30 INPUT "Montant de la vente ";SalesAmount
-
- 40 PRINT "Le montant de la vente avec taxe est "; SalesAmount * TaxRate
- 50 TotalAmount = SalesAmount + SalesTax
-
- 60 PRINT
- 70 PRINT "Le montant de la vente est : ";TAB(30); SalesAmount
-
- 80 PRINT "Le montant de la taxe de vente est ";TAB(30); SalesTax
-
- 90 PRINT "Le montant total est ";TAB(30); TotalAmount
- La ligne 40 calcule la taxe de vente et l'affecte à la valeur de SalesTax.
- La ligne 50 calcule le montant total de la vente et l'affecte à la valeur de TotalAmount.
- La ligne 60 est une instruction PRINT «vide». Elle provoque l'affichage d'une ligne vierge. Vous pouvez contrôler et améliorer l'apparence des résultats affichés en utilisant les instructions PRINT de manière appropriée.
- Aux lignes 70, 80 et 90, la fonction TAB indique à l'ordinateur de déplacer le curseur vers la colonne spécifiée entre parenthèses. «TAB(30)» déplace le curseur vers la colonne 30.
Entrez et enregistrez ce programme sous le nom GWSM0004, puis exécutez-le. Un exemple d'exécution est présenté ici :
|
Montant de la vente ? 1 Le montant de la vente est 1 Le montant de la taxe de vente est .06 Le montant total est 1.06 |
Remarque : à partir de maintenant, le prompt GW-BASIC (Ok) et le curseur (_) seront omis lors de l'affichage des résultats de l'exécution d'un programme.
L'instruction PRINT USING
Bien que les valeurs de SalesAmount, SalesTax et TotalAmount soient toutes affichées à partir de la colonne 30, les décimales ne s'alignent pas correctement. Pour résoudre ce problème, utilisez une variante de l'instruction d'impression appelée PRINT USING. L'instruction PRINT USING vous permet de spécifier l'apparence et le positionnement des nombres. Elle permet également d'arrondir les nombres à un nombre donné de décimales.
L'instruction suivante indique à l'ordinateur d'afficher la valeur de SalesAmount avec jusqu'à cinq chiffres avant la virgule décimale et deux chiffres après la virgule décimale, arrondis si nécessaire :
| PRINT USING "#####.##"; SalesAmount |
- 1 REM ** Taxe de vente étendu **
- 2 ' GW-BASIC, fichier : GWSM0005
-
- 10 CLS
- 20 TaxRate = 6 / 100
-
- 30 INPUT "Montant de la vente ";SalesAmount
-
- 40 SalesTax = SalesAmount * TaxRate
- 50 TotalAmount = SalesAmount + SalesTax
-
- 60 PRINT
- 70 PRINT "Le montant de la vente est : ";TAB(30)
- 75 PRINT USING "#####.##"; SalesAmount
-
- 80 PRINT "Le montant de la taxe de vente est : ";TAB(30)
- 85 PRINT USING "#####.##"; SalesTax
-
- 90 PRINT "Le montant total est : ";TAB(30)
- 95 PRINT USING "#####.##"; TotalAmount
Le programme GWSM0005 utilise trois instructions PRINT USING, aux lignes 75, 85 et 95.
Entrez et enregistrez ce programme sous le nom GWSM0005, puis exécutez-le. Étant donné que les trois nombres sont affichés avec la même chaîne de caractères de format PRINT USING ("#####.##"), ils s'alignent verticalement le long de la virgule décimale, comme indiqué dans les deux exécutions suivantes :
|
Montant de la vente ? 1 Le montant de la vente est : 1.00 Le montant de la taxe de vente est : 0.06 Le montant total est : 1.06 Montant de la vente ? 29.95 Le montant de la vente est : 29.95 Le montant de la taxe de vente est : 1.80 Le montant total est : 31.75 |
La paire d'instructions suivante affiche une ligne sur l'écran :
La ligne 70 affiche la chaîne de caractères «Le montant de la vente est :», puis passe à la colonne 30. Le point-virgule à la fin de la ligne 70 maintient le curseur à la colonne 30 ; de sorte que les informations affichées par la ligne 75 commenceront à cet endroit. La ligne 75 affiche la valeur de SalesAmount telle que spécifiée par la chaîne de caractères de format, «#####.##». Par exemple :
- Afficher par la ligne 70 : «Le montant de la vente est :».
- Afficher par la ligne 75 : «29.95».
Les lignes 80 et 85 fonctionnent également ensemble pour produire une ligne d'affichage, tout comme les lignes 90 et 95.
Notez que tous les nombres sont affichés avec deux décimales, comme spécifié par la chaîne de caractères de format ("#####.##") dans les instructions PRINT USING. La chaîne de caractères de format limite le nombre affiché à cinq chiffres maximum avant la virgule décimale. Si un nombre affiché est supérieur à 99999,99, un signe de pourcentage (%) est affiché devant le nombre, comme indiqué ici :
|
Montant de la vente ? 1000000 Le montant de la vente est : %100000.00 Le montant de la taxe de vente est : 60000.00 Le montant total est : %1060000.00 |
Ce programme a une solution simple. Utilisez des variables à double précision et des chaînes de caractères de format autorisant plus de chiffres avant la virgule décimale, comme illustré par le programme GWSM0006 :
- 1 REM ** Taxe de vente étendu **
- 2 ' GW-BASIC, fichier : GWSM0006
-
- 10 CLS
- 20 TaxRate# = 6 / 100#
-
- 30 INPUT "Montant de la vente ";SalesAmount#
-
- 40 SalesTax# = SalesAmount# * TaxRate#
- 50 TotalAmount# = SalesAmount# + SalesTax#
-
- 60 PRINT
- 70 PRINT "Le montant de la vente est : ";TAB(30)
- 75 PRINT USING "############.##"; SalesAmount#
-
- 80 PRINT "Le montant de la taxe de vente est : ";TAB(30)
- 85 PRINT USING "############.##"; SalesTax#
-
- 90 PRINT "Le montant total est : ";TAB(30)
- 95 PRINT USING "############.##"; TotalAmount#
Entrons et sauvegardons le programme GWSM0006, puis exécutons-le pour un montant de vente vraiment important, un milliard de dollars (1000000000000), comme le montre l'exemple suivant :
|
Montant de la vente ? 1000000000000 Le montant de la vente est : 1000000000000.00 Le montant de la taxe de vente est : 60000000000.00 Le montant total est : 1060000000000.00 |
Dans le programme GWSM0006, notez les éléments suivants :
- Les variables à double précision TaxRate#, SalesAmount#, SalesTax# et TotalAmount#.
- À la ligne 20, un nombre à double précision (100#) est utilisé pour garantir que la valeur de TaxRate# sera aussi précise que possible. Les nombres dans GW-BASIC sont entreposés sous forme de nombres binaires (base 2). Le nombre décimal .06 ne peut pas être entreposé exactement sous forme de nombre binaire ; une petite «erreur d'arrondi» se produit. Cette erreur est bien moindre si le calcul est effectué à l'aide d'un nombre à double précision. Une description complète de l'erreur d'arrondi dépasse le cadre de cette page.
- La chaîne de format (############.##) dans les instructions PRINT USING autorise jusqu'à 12 chiffres avant la virgule décimale.
Autres fonctionnalités de PRINT USING
L'instruction de format PRINT USING possède de nombreuses variantes. Parmi les plus utiles, on trouve l'impression de signes dollar ($) avant les nombres, l'insertion automatique de signes dollar ($) avant les nombres et l'insertion automatique de virgules dans les très grands nombres. Ces fonctionnalités sont présentées aux lignes 75, 85 et 95 du programme GWSM0007 :
- 1 REM ** Taxe de vente étendu **
- 2 ' GW-BASIC, fichier : GWSM0007
-
- 10 CLS
- 20 TaxRate# = 6 / 100#
-
- 30 INPUT "Montant de la vente ";SalesAmount#
-
- 40 SalesTax# = SalesAmount# * TaxRate#
- 50 TotalAmount# = SalesAmount# + SalesTax#
-
- 60 PRINT
- 70 PRINT "Le montant de la vente est : ";TAB(30)
- 75 PRINT USING "$$###,###,###,###.##"; SalesAmount#
-
- 80 PRINT "Le montant de la taxe de vente est : ";TAB(30)
- 85 PRINT USING "$$###,###,###,###.##"; SalesTax#
-
- 90 PRINT "Le montant total est : ";TAB(30)
- 95 PRINT USING "$$###,###,###,###.##"; TotalAmount#
Modifiez le programme GWSM0006 pour créer le programme GWSM0007, enregistrez le programme modifié et exécutez-le. Voici un exemple d'exécution. Notez le signe dollar ($) avant chaque nombre et les virgules intégrées dans la partie du nombre à gauche de la virgule décimale :
|
Montant de la vente ? 1000000000000 Le montant de la vente est : $1,000,000,00,000.00 Le montant de la taxe de vente est : 60,000,000.00 Le montant total est : 1,060,000,000.00 |
La chaîne de format "$$###,###,###,###.##" indique à l'ordinateur d'afficher un nombre comme suit :
- Le double signe dollar ($$) entraîne l'affichage d'un signe dollar à gauche du nombre.
- Les 12 signes numériques (#) séparés par des virgules permettent d'afficher jusqu'à 12 chiffres du nombre, avec des virgules insérées tous les trois chiffres. Si moins de 12 chiffres sont affichés, des espaces sont affichés à la place, dans ce cas à gauche du signe dollar.
- Le point décimal entraîne l'affichage d'un point décimal dans le nombre.
- Les deux signes numériques à droite du point décimal entraînent l'impression de deux chiffres à droite du point décimal. Si nécessaire, le nombre affiché est arrondi à deux chiffres.
Valeur des actions
Si vous possédez des actions, le programme suivant pourrait vous être utile. Il calcule et affiche la valeur d'un bloc d'actions, en fonction du nombre d'actions et du prix par action :
Saisissez et enregistrez le programme GWSM0008 (Valeur des actions), puis exécutez-le. Un exemple d'exécution est présenté ici :
|
Nombre d'actions? 1200 Prix par action? 37.50 La valeur est $45,000.00 |
La chaîne de caractères de format "$$############,.##" est équivalente à la chaîne de caractères de format "$$###,###,###,###.##" utilisée précédemment dans le programme GWSM0007. Dans les deux cas, des virgules sont affichées tous les trois chiffres dans la partie du nombre à gauche de la virgule décimale.
N'oubliez pas : un signe dièse (#) à la fin d'un nom de variable définit la variable comme une variable à double précision.
Le programme GWSM0008 utilise les variables à double précision suivantes :
- NumberOfShares#
- PricePerShare#
- Value#
Une variable à double précision fournit environ 16 chiffres de précision. Essayez le programme avec des nombres très grands. Que se passe-t-il lorsque la valeur de Value# est supérieure à la limite imposée par la chaîne de caractères de format PRINT USING ? Essayez-le et découvrez-le. Essayez également d'autres chaînes de caractères de format, peut-être une permettant l'affichage de nombres encore plus grands. La chaîne de caractères de format du programme permet l'affichage de montants allant jusqu'à $999,999,999,999.99.
Un programme de valeur future - intérêt composé
Supposons que vous déteniez votre argent sur un compte bancaire versant des intérêts réguliers, composés périodiquement. Le programme GWSM0009 calcule la valeur de l'argent (capital) investi à un taux d'intérêt particulier par période, composé pour un nombre donné de périodes :
- 1 REM ** Valeur future de l'argent - Intérêts composés **
- 2 ' GW-BASIC, fichier : GWSM0009
-
- 100 REM ** Efface l'écran **
- 110 CLS
-
- 200 REM ** Obtenir le capital, le taux d'intérêt et le nombre de périodes **
- 210 INPUT "Montant principal investi ($)"; Principal#
- 220 INPUT "Taux d'intérêt par période (%) "; Rate#
- 230 INPUT "Nombre de périodes d'intérêt "; Periods#
-
- 300 REM ** Calculer la valeur future **
- 310 Rate# = Rate# / 100
- 320 FutureValue# = Principal# * (1 + Rate#) ^ Periods#
-
- 400 REM ** Afficher la valeur future **
- 410 PRINT
- 420 PRINT "A l'échéance, la valeur sera ";
- 430 PRINT USING "$$############,.##"; FutureValue#
Examinez les exécutions suivantes et réfléchissez à la manière dont vous écririez le programme. Le premier échantillon concerne 1 $ investi à 1% d'intérêt, composé sur une période. Il est utilisé pour tester le programme. La réponse devrait être 1,01 $ :
|
Montant principal investi ($) ? 1 Taux d'intérêt par période (%) ? 1 Nombre de périodes d'intérêt ? 1 A l'échéance, la valeur sera $1.01 |
Supposons maintenant que vous avez un solde de 500 $ sur une carte de crédit facturant 1,5 % d'intérêt par mois et que vous reportez son paiement pendant 12 mois.
|
Montant principal investi ($) ? -500 Taux d'intérêt par période (%) ? 1.5 Nombre de périodes d'intérêt ? 12 A l'échéance, la valeur sera $597.81 |
L'«investissement» est saisi sous la forme -500 pour vous rappeler que vous possédez 500 $ et que vous payez donc les intérêts. Le résultat est -597,81 $.
Il peut être utile de rédiger d'abord un aperçu du programme dans les déclarations REM. La liste suivante montre un aperçu possible :
- 1 REM ** Valeur future de l'argent - Intérêts composés **
- 2 ' GW-BASIC, fichier : GWSM0009
-
- 100 REM ** Efface l'écran **
-
- 200 REM ** Obtenir le capital, le taux d'intérêt et le nombre de périodes **
-
- 300 REM ** Calculer la valeur future **
-
- 400 REM ** Afficher la valeur future **
Une fois que vous avez défini les grandes lignes de votre programme, vous pouvez le développer comme indiqué dans le programme GWSM0009.
Le programme comporte cinq blocs. Chaque bloc commence par une instruction REM indiquant ce que fait le bloc. Le premier bloc (1 REM) indique le nom du programme, l'endroit où il a été publié pour la première fois et le nom du fichier du programme tel qu'il est entreposé sur un disque.
Le deuxième bloc (100 REM) efface l'écran ; s'il y a d'autres configurations de programme à effectuer, ce bloc inclura également ces instructions.
Le troisième bloc (200 REM) utilise l'instruction INPUT pour obtenir les valeurs des trois variables utilisées pour calculer le montant des intérêts et la valeur future. Toutes les variables sont en double précision, ce qui est utile pour gérer des valeurs importantes.
- Princpal# est le montant investi, en dollars et en cents.
- Rate# est le taux d'intérêt par période d'intérêt. Entrez 1 pour 1 %, 1,5 pour 1,5 %, ...
- Period# est le nombre de périodes sur lesquelles l'intérêt est composé. Par exemple, si les intérêts sont composés mensuellement pendant un an, entrez 12 comme valeur de Period#.
Le quatrième bloc (300 REM) calcule la valeur future. Le taux d'intérêt est d'abord converti en fraction décimale (ligne 310), étant utilisée dans la formule pour calculer la valeur future. Notez l'utilisation de l'opérateur d'exponentielle (^). Dans un livre de mathématiques, vous pourriez voir une formule d'intérêt composé telle que celle présentée ici :
| A = P(1 + r)n |
où P est le capitale, placé à un taux d'intérêt r pendant n périodes, produisant un montant A (valeur future).
En GW-BASIC, la formule s'écrirait ainsi :
| A = P * (1 + r)^n |
Dans cette page, des variables plus descriptives sont utilisées afin de rendre les programmes plus faciles à comprendre. La variable Principal# est plus descriptive que la lettre P.
Le cinquième et dernier bloc (REM) affiche la valeur de la valeur future, précédée de la chaîne de caractères «À l'échéance, la valeur sera de». La chaîne de caractères de format «$$############,.##» entraîne l'affichage du nombre avec un signe dollar et des virgules tous les trois chiffres.
Une variante du programme est présentée ci-après sous le nom GWSM0009 (Valeur future de l'argent - Intérêts composés #2). Il demande le capitale, le taux d'intérêt annuel, le nombre de fois par an où les intérêts sont composés et le nombre de périodes d'intérêt. Voici quatre exemples d'exécutions pour illustrer l'utilité de ce programme :
- 1 REM ** Valeur future de l'argent - Intérêts composés #2 **
- 2 ' GW-BASIC, fichier : GWSM0010
- 3 ' Calculez la valeur future de l'argent investi à un taux d'intérêt annuel et composé une ou plusieurs fois par an.
-
- 100 REM ** Efface l'écran ***
- 110 CLS
-
- 200 REM ** Obtenir le capital, le taux d'intérêt et le nombre de périodes **
- 210 INPUT "Montant principal investi ($) "; Principal#
- 220 INPUT "Taux d'intérêt par an (%) "; YearlyRate#
- 230 INPUT "Période d'intérêt par an "; PeriodsPerYear#
- 240 INPUT "Nombre de périodes d'intérêt "; Periods#
-
- 300 REM ** Calculer la valeur future **
- 310 Rate# = YearlyRate# / PeriodsPerYear# / 100
- 320 FutureValue# = Principal# * (1 + Rate#) ^ Periods#
-
- 400 REM ** Afficher la valeur future **
- 410 PRINT
- 420 PRINT "A l'échéance, la valeur sera";
- 430 PRINT USING "$$############,.##"; FutureValue#
Les exemples d'exécution concernent un investissement de 1 000 $ à 12 % par an. L'exemple d'exécution n° 1 est composé annuellement. L'exemple d'exécution n° 2 est composé mensuellement. L'exemple d'exécution n° 3 est composé hebdomadairement et l'exemple d'exécution n° 4 est composé quotidiennement :
|
Montant principal investi ($) ? 1000 Taux d'intérêt par an (%) ? 12 Période d'intérêt par an ? 1 Nombre de périodes d'intérêt ? 1 A l'échéance, la valeur sera $1,120.00 |
Exemple d'exécution n° 2 :
|
Montant principal investi ($) ? 1000 Taux d'intérêt par an (%) ? 12 Période d'intérêt par an ? 12 Nombre de périodes d'intérêt ? 12 A l'échéance, la valeur sera $1,126.82 |
Exemple d'exécution n° 3 :
|
Montant principal investi ($) ? 1000 Taux d'intérêt par an (%) ? 12 Période d'intérêt par an ? 52 Nombre de périodes d'intérêt ? 52 A l'échéance, la valeur sera $1,127.34 |
Exemple d'exécution n° 4 :
|
Montant principal investi ($) ? 1000 Taux d'intérêt par an (%) ? 12 Période d'intérêt par an ? 365 Nombre de périodes d'intérêt ? 365 A l'échéance, la valeur sera $1,127.48 |
Supposons que les intérêts soient composés toutes les heures, 24 heures sur 24, pendant un an. Utilisez une instruction PRINT directe pour calculer le nombre de périodes d'intérêt :
Type :
| PRINT 24*365 |
Il affiche :
8760Utilisez maintenant cette valeur lorsque vous exécutez le programme. Essayez également de capitaliser toutes les minutes et toutes les secondes pendant un an. Utilisez une instruction PRINT directe pour calculer le nombre de périodes d'intérêt. Gagnez-vous beaucoup en capitalisant plus fréquemment ?
Impression sur l'imprimante
Dans la page Introduction à la programmation, vous avez appris à utiliser l'instruction LLIST pour lister un programme sur l'imprimante. Vous pouvez également utiliser LPRINT ou LPRINT USING dans un programme pour imprimer des informations sur l'imprimante. Dans le programme GWSM0010, modifiez le bloc 1 et ajoutez le bloc 500, comme indiqué ici :
- 1 REM ** Valeur future de l'argent - Intérêts composés #3 **
- 2 ' GW-BASIC, fichier : GWSM0011
- 3 ' Calculez la valeur future de l'argent investi à un taux d'intérêt annuel et composé une ou plusieurs fois par an.
- 4 ' La sortie est à la fois sur écran et sur imprimante
-
- 100 REM ** Efface l'écran ***
- 110 CLS
-
- 200 REM ** Obtenir le capital, le taux d'intérêt et le nombre de périodes **
- 210 INPUT "Montant principal investi ($) "; Principal#
- 220 INPUT "Taux d'intérêt par an (%) "; YearlyRate#
- 230 INPUT "Période d'intérêt par an "; PeriodsPerYear#
- 240 INPUT "Nombre de périodes d'intérêt "; Periods#
-
- 300 REM ** Calculer la valeur future **
- 310 Rate# = YearlyRate# / PeriodsPerYear# / 100
- 320 FutureValue# = Principal# * (1 + Rate#) ^ Periods#
-
- 400 REM ** Afficher la valeur future **
- 410 PRINT
- 420 PRINT "A l'+?ch+?ance, la valeur sera";
-
- 500 REM ** Imprimer toutes les valeurs sur l'imprimante **
- 510 LPRINT "Montant principal investi"; TAB(32);
- 515 LPRINT USING "$$############,.##"; Principal#
- 520 LPRINT "Taux d'intérêt par an (%) "; TAB(34);
- 525 LPRINT USING "############,.##"; YearlyRate#
- 540 LPRINT "Taux d'intérêt par an (%) ";TAB(34);
- 545 LPRINT USING "############,.##"; Periods#
- 550 LPRINT "Nombre de périodes d'intérêt "; TAB(34);
- 560 LPRINT
- 570 LPRINT "A l'échéance, la valeur sera"; TAB(32);
- 575 LPRINT USING "$$############,.##"; FutureValue#
- 580 LPRINT : LPRINT : LPRINT
- 590 END
Notez que les doubles signes dollar ($$) ne sont pas utilisés dans l'instruction LPRINT USING pour les valeurs des variables YearRate# et Periods#.
Étant donné que les doubles signes dollar entraînent l'impression d'un espace et d'un signe dollar, la valeur TAB est modifiée de 32 à 34 pour l'impression formatée de «Taux d'intérêt par an», «Périodes d'intérêt par an» et «Nombre de périodes d'intérêt».
Sauvegardez le programme modifié sous le nom de fichier GWSM0011, puis exécutez-le. Les informations apparaîtront à l'écran comme avant, ainsi que sur l'imprimante, comme indiqué ici :
|
Montant principal investi ($) ? 1000,00 Taux d'intérêt par an (%) ? 12 Période d'intérêt par an ? 12 Nombre de périodes d'intérêt ? 12 A l'échéance, la valeur sera $1,126.82 |
N'oubliez pas :
- Pour lister un programme sur l'imprimante, utilisez LLIST.
- Pour imprimer des chaînes et des nombres sur l'imprimante à partir d'un programme, utilisez PRINT ou PRINT USING.
Révision
Utilise les opérateurs arithmétiques (+, -, *, /) et l'opérateur d'exponentielle (^) pour effectuer des calculs. Vous pouvez le faire avec des instructions directes ou au moyen d'un programme. Le GW-BASIC fournit trois types de nombres que vous pouvez utiliser pour le traitement des nombres :
- Un entier est un nombre entier compris entre -32 768 et 32 767. Un entier n'a pas de point décimal. Vous pouvez utiliser un signe de pourcentage (%) pour désigner un nombre comme entier.
- Un nombre à simple précision est un entier ou un non entier comportant jusqu'à sept chiffres et un point décimal. Si un nombre est trop grand pour être présenté en sept chiffres, il est exprimé sous la forme d'un nombre à virgule flottante avec une mantisse et un exposant, séparés par la lettre E. Vous pouvez utiliser un point d'exclamation (!) pour désigner un nombre comme un nombre à simple précision.
- Un nombre à double précision est un entier ou un non entier comportant jusqu'à 16 chiffres et un point décimal. Si un nombre est trop grand pour être représenté en 16 chiffres, il est exprimé sous la forme d'un nombre à virgule flottante double précision avec une mantisse et un exposant, séparés par la lettre D. Vous pouvez utiliser un signe dièse (#) pour désigner un nombre comme un nombre double précision.
Une variable numérique est l'étiquette, ou le nom, d'une «case numérique» dans laquelle un nombre peut être entreposé. Un nom de variable peut être n'importe quelle combinaison de lettres et de chiffres d'une longueur maximale de 40 caractères. Le premier caractère doit être une lettre. Le GW-BASIC ne fait pas de distinction entre les lettres majuscules et minuscules dans les noms de variables : par exemple, pi, Pi et PI sont identiques. Utilisez %, ! ou # pour désigner les variables comme étant respectivement entières, à simple précision ou à double précision. Le GW-BASIC suppose qu'une variable non désignée est à simple précision. Utilisez l'instruction INPUT pour acquérir les valeurs des variables. Vous pouvez inclure une chaîne de caractères dans l'instruction INPUT pour identifier les informations requises.
Utilisez les instructions PRINT et PRINT USING pour afficher des informations à l'écran. Utilisez les instructions LPRINT et LPRINT USING pour imprimer des informations sur l'imprimante.
Incluez les instructions REM dans les programmes pour les rendre plus faciles à lire et à comprendre. Vous pouvez utiliser une apostrophe (') comme abréviation de REM. Vous pouvez même utiliser l'instruction REM pour rédiger un aperçu d'un programme avant d'écrire le programme complet. Cela vous fera gagner beaucoup de temps.