Génération de cercle
La génération de cercle est une opération basé sur équation cartésienne ayant évolué pour finalement utilisé un algorithme de Bresenham. Voici les différents algorithmes, en commençant par les plus anciens et les moins efficace jusqu'au plus récent et les plus efficace.
Équation cartésienne d'un cercle
En mathématique, on peut générer un cercle en se basant sur la formule des carrés, soit :
|
(X - Xc)2 + ( Y - Yc )2 = R2 ⇒ Y = Yc ± √ R2 - (X - Xc)2 |
On arrivera donc à l'algorithme cartésien suivant :
|
MODULE Cercle(valeur X, valeur Y, valeur Rayon) BOUCLE POUR x ← -R JUSQU'A R Affiche Point ( X, +Y ) Affiche Point ( X, -Y) FIN BOUCLE |
Cette algorithme à de nombreuses lacunes comme par exemple, il est possible qu'il y est des espacements entre les points et il demande un nombre de calcul très important.
Équation paramétrique (polaire) d'un cercle
En mathématique, on peut déduire l'équation paramétrique ou équation polaire d'un cercle grâce à la formule suivante :
|
X = Xc + R COS θ Y = Yc + R SIN θ |
En se basant sur la formule mathématique précédente, on peut arriver à un algorithme affichant un cercle avec le nombre PI (3,14≈), c'est-a-dire en utilisant les fonctions COS et SIN des mathématiques. Bien que cette technique soit très peut efficace par rapport à l'algorithme de Bresenham, elle en demeure pas moins facile à comprendre et à imaginer. Voici donc son algorithme :
|
MODULE COS(X) R ← X x X S ← 42.0 BOUCLE POUR I ← 10 JUSQU'A 1 S ← 4.0 x I - 2.0 + (-R) / S FIN BOUCLE POUR S ← S x S RETOURNE (S - R) / (S + R) MODULE SIN(X) R ← X x X S ← 42.0 BOUCLE POUR I ← 10 JUSQU'A 1 S ← 4.0 x I - 2.0 + (-R) / S FIN BOUCLE POUR RETOURNE 2.0 x X x S / (R + S x S) MODULE Cercle(valeur X, valeur Y, valeur Rayon) Fin ← PI / 2 Pente ← X / Y Saute ← Fin / ( R x 2 x Pente ) BOUCLE POUR Degré ← 0 JUSQU'A Fin AVEC SAUT DE Saute A ← COS(Degré) x Rayon x Pente B ← SIN(Degré) x Rayon x Pente Affiche Point ( X + A, Y + B ) Affiche Point ( X + A, Y - B ) Affiche Point ( X - A, Y + B ) Affiche Point ( X - A, Y - B ) FIN BOUCLE |
Cette algorithme est plus fiable que la précédente, mais effectue un grand nombre de calcul et il faut compléter les segments de droite.
Algorithme de Bresenham
L'algorithme le plus efficace est sans nulle doute celui publié en 1977 par Bresenham dans son livre. Il est basé sur son travail précédent baptisé tracé de segments et de l'algorithme de Pitteway sur le tracé des coniques. L'idée derrière est la suivante : il faut toujours se basé sur le choix entre 2 points discrets et de leur dépendance de leur distance respective avec un point réel. Par la suite, on travail dans le deuxième octant à partir du point (0,r) ainsi que pour un point (xi,yi) avec le prochain point allant être respectivement (xi,yi ou (xi+1,yi+1,yi-1). Ensuite, on calcul le y suivant et les leurs différences avec les points discrets de la manière suivante :
|
Y2 = R2 - (Xi + 1)2 d1 = Yi2 - Y2 = Yi2 - R2 + (Xi + 1)2 d2 = Y2 - (Yi - 1)2 = R2 - (Xi + 1)2 - (Yi - 1)2 |
Ensuite, la formule mathématique permet de déterminer la direction du points (latéral ou diagonale) :
| pi = (d1 - d2) = 2(xi + 1)2 + Yi2 + (yi - 1)2 - 2r2 |
En se basant sur ces formulaires mathématique, on aura donc un algorithme ressemblant à ceci :
|
MODULE Cercle(x,y,Rayon,LineWidth) x1 ← x - Rayon y1 ← y - Rayon x2 ← x + Rayon y2 ← y + Rayon y ← y1 y1 ← y2 y2 ← y yr ← Rayon xr ← Rayon xN ← x2 - xr yN ← y2 + yr Rayon ← Rayon - LineWidth / 2 a ← Rayon BOUCLE POUR i ← 0 JUSQU'A LineWidth SAUT 1 BO ← Rayon x Rayon AO ← a x a y ← Rayon x ← 0 AO2 ← AO x 2 AO4 ← AO x 4 BO2 ← BO x 2 BO4 ← BO x 4 d ← AO2 x (y-1) x y + AO + BO2 x (1-AO) BOUCLE FAIRE TANT QUE AO x y > BO x x Affiche Point (x+xN,yN-y) Affiche Point (x+xN,y1-yr+y) Affiche Point (x1+xr-x,yN-y) Affiche Point (x1+xr-x,y1-yr+y) SI d >= 0 ALORS y ← y - 1 d ← d - AO4 x y FIN SI d ← d + BO2 x (3 + (x x 2)) x ← x + 1 FIN BOUCLE FAIRE TANT QUE d ← BO2 x (x+1) x x + AO2 x (y x (y-2) + 1) + (1-AO2) x BO BOUCLE FAIRE TANT QUE y ≠ 0 Affiche Point (x+xN,yN-y) Affiche Point (x+xN,y1-yr+y) Affiche Point (x1+xr-x,yN-y) Affiche Point (x1+xr-x,y1-yr+y) SI d <=0 ALORS x ← x + 1 d ← d + BO4 x x FIN SI y ← y - 1 d ← d + AO2 x (3-(y x 2 )) FIN BOUCLE TANT QUE Rayon ← Rayon + 1 a ← a + 1 FIN BOUCLE POUR |
Exemple
En se basant sur l'algorithme de Bresenham, on peut facilement écrire un programme JavaScript fonctionnant sur des navigateurs Web comme Internet Explorer, Netscape, Firefox et Opera, de la façon suivante :
- <HTML>
- <HEAD>
- <SCRIPT LANGUAGE="JavaScript1.2">
- function SetPixel(x,y,Kr) {
- var html = '';
- html += '<SPAN';
- html += ' STYLE="position: absolute; visibility: inherit;';
- html += ' left: ' + x + 'px; top: ' + y + 'px;';
- html += ' width: ' + this.dotSize + 'px; height: ' + this.dotSize + 'px;';
- html += ' background-color: ' + Kr + ';';
- html += document.all ? 'clip: rect (0 ' + this.dotSize + ' ' + this.dotSize + ' 0);' : '';
- html += '"';
- html += '>';
- html += '<\/SPAN>';
-
- html += '<DIV ID="Pixel' + this.id + '"';
- html += ' STYLE="position: absolute;';
- html += ' left: ' + x + 'px; top: ' + y + 'px;';
- html += ' width: ' + 1 + 'px; height: ' + 1 + 'px;';
- html += ' background-color: ' + Kr + ';';
- html += '"';
- html += '><FONT SIZE="-3"></FONT>';
- html += '<\/DIV>';
-
- document.write(html);
- }
-
- function Circle(x,y,Rayon,LineWidth,Kr) {
- x1=x-Rayon;y1=y-Rayon;x2=x+Rayon;y2=y+Rayon;
- y=y1;y1=y2;y2=y;yr=Rayon;xr=Rayon;xN=x2-xr;yN=y2+yr;
- Rayon-=LineWidth >> 1;a=Rayon;
- for(i=0;i<LineWidth;i++) {
- BO=Rayon*Rayon;AO=a*a;y=Rayon;x=0;
- AO2=AO << 1;
- AO4=AO << 2;
- BO2=BO << 1;
- BO4=BO << 2;
- d=AO2*(y-1)*y+AO+BO2*(1-AO);
- while(AO*y>BO*x) {
- SetPixel(x+xN,yN-y,Kr);
- SetPixel(x+xN,y1-yr+y,Kr);
- SetPixel(x1+xr-x,yN-y,Kr);
- SetPixel(x1+xr-x,y1-yr+y,Kr);
- if(d>=0) {
- y--;
- d-=AO4*y;
- }
- d+=BO2*(3+(x << 1));
- x++;
- }
- d=BO2*(x+1)*x+AO2*(y*(y-2)+1)+(1-AO2)*BO;
- while(y!=0) {
- SetPixel(x+xN,yN-y,Kr);
- SetPixel(x+xN,y1-yr+y,Kr);
- SetPixel(x1+xr-x,yN-y,Kr);
- SetPixel(x1+xr-x,y1-yr+y,Kr);
- if(d<=0) {
- x++;
- d+=BO4*x
- }
- y--;
- d+=AO2*(3-(y << 1));
- }
- Rayon++;a++;
- }
- }
-
- Circle(55,55,45,1,"#00FF00");
-
- </SCRIPT>
- </HEAD>
- <BODY>
- Bonjour!!!
- </BODY>
- </HTML>
on obtiendra le résultat suivant :
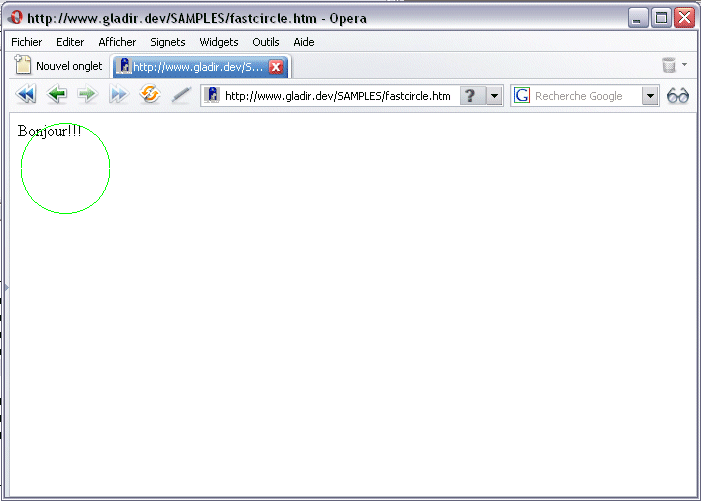
Voir également
Langage de programmation - JavaScript - Affichage & Graphique - Cercle