La bibliothèque SANE
Cette annexe décrit le SANE (Standard Apple Numeric Environment) et les routines contenues dans les bibliothèques SANE SANELib.o et SANELib881.o. Il contient deux parties :
- une discussion sur les types de données fournis par SANE
- une description de chacun des types, procédures et fonctions contenus dans les bibliothèques SANE
SANE est la base des calculs mathématiques à virgule flottante effectués par MPW Pascal. Il répond à toutes les exigences en matière d'arithmétique à virgule flottante de précision étendue, telles que prescrites par les normes IEEE 754 et 854. Il garantit que toutes les opérations en virgule flottante sont effectuées de manière cohérente et qu'elles renvoient les résultats les plus précis possibles.
SANE fournit un environnement flexible et facile à utiliser pour les calculs en virgule flottante. Il vous donne des résultats extrêmement précis sans codage supplémentaire. Vous pouvez écrire des programmes ANS Pascal standard en utilisant uniquement le type réel et être sûr que vos résultats sont aussi précis que possible dans ce format.
Si vous êtes intéressé par une précision au-delà de celle possible en utilisant uniquement le type réel, vous pouvez utiliser les autres types à virgule flottante fournis comme extension de Pascal par SANE. De plus, la bibliothèque SANE contient des fonctions numériques introuvables dans le Pascal standard et des routines permettant de contrôler l'environnement dans lequel les calculs en virgule flottante sont effectués.
Cette annexe présente la version de SANE disponible sur tous les Macintosh. Sur les Macintosh équipés d'un 68020 et d'un 68881 (comme le Macintosh II), les paquets SANE peuvent appeler le 68881 pour les fonctions arithmétiques de base. Cette annexe fournit également des informations sur les 68881 fonctions transcendantales.
Les types de données SANE
La spécification originale de Pascal n'appelait qu'un seul type de données à utiliser avec les nombres à virgule flottante : le type réel. Le MPW Pascal étend le langage de programmation avec quatre types : single, double, extended et comp.
Remarque : La norme ANSI spécifie que toute implémentation de Pascal répondant à ses critères ; les exigences doivent inclure un type nommé real. Le type unique MPW Pascal et le type réel ANS Pascal sont synonymes. Le compilateur MPW Pascal acceptera l'un ou l'autre de ces termes et les traitera exactement de la même manière.
Descriptions des types
Le type unique est le plus petit format utilisé avec les nombres à virgule flottante. Il entrepose les nombres à virgule flottante en utilisant 32 bits d'entreposage.
Le type double est deux fois plus grand que le type single. Il utilise 64 bits pour l'entreposage.
Le type étendu est encore plus grand : il utilise un format 80 bits. Toutes les arithmétiques impliquant des valeurs de type real sont effectuées en utilisant le type étendu. Le type extended occupe 96 bits lorsque l'option -MC68881 est appelée.
Le type comp entrepose les valeurs intégrales au format 64 bits. Il est classé comme un type real car l'arithmétique à précision étendue est effectuée avec des opérandes de type comp et utilise le type extended. Les résultats affectés à une variable de type comp sont convertis depuis extended.
Les types single, double et extended sont définis par la norme IEEE.
Choisir un type de données
En règle générale, le choix d'un type de données nécessite que vous déterminiez les compromis entre :
- Forme à virgule fixe et à virgule flottante
- précision
- intervalle
- utilisation de la mémoire
La précision, l'intervalle et l'utilisation de la mémoire pour chaque type de données SANE sont indiquées dans le tableau suivant :
| Identificateur de type | Single | Double | Comp | Extended * |
|---|---|---|---|---|
| Taille (octets : bits) | 4:32 | 8:64 | 8:64 | 10:80 |
| Intervalle d'exposant binaire | ||||
| Minimum | -126 | -1022 | - | -16383 |
| Maximum | 127 | 1023 | - | 16383 |
| Précision significative | ||||
| Bits | 24 | 53 | 63 | 64 |
| Chiffres décimaux | 7 à 8 | 15 à 16 | 18 à 19 | 19 à 20 |
| Intervalle décimale (approximative) | ||||
| Minimum négatif | -3.4E+38 | -1.7E+308 | -9.2E18 | -1.1E+4932 |
| Norme négative maximale | -1.2E-38 | -2.3E-308 | -1.7E-4932 | |
| Dénormation négative maximale | -1.5E-45 | -5.0E-324 | -1.9E-4951 | |
| Dénorme positive minimale | 1.5E-45 | 5.0E-324 | 1.9E-4951 | |
| Norme minimale positive | 1.2E-38 | 2.3E-308 | 1.7E-4932 | |
| Positif maximum | 3.4E+38 | 1.7E+308 | ≈9.2E18 | 1.1E+4932 |
| Infinis | Oui | Oui | Non | Oui |
| Pas un Nombre (NaN) | Oui | Oui | Oui | Oui |
* Lorsque -MC68881 est appelé, le type étendu occupe 12 octets, soit 96 bits. Il n'y a aucun autre changement dans les types de données dans ce tableau.
De nombreux programmes nécessitent un type de comptage comptant exactement les choses (centimes, dollars, widgets). En utilisant SANE, vous pouvez écrire un programme traitant les valeurs monétaires en représentant ces valeurs sous forme de nombres entiers de cents ou de mils, pouvant être entreposés exactement dans le type comp. La somme, la différence ou le produit de deux valeurs de comparaison est exact si l'ampleur du résultat ne dépasse pas 263-1 (c'est-à-dire 9223372036854775807). De plus, les valeurs comp (par exemple, les résultats des calculs comptables) peuvent être mélangées avec des valeurs étendues dans les calculs à virgule flottante (comme les intérêts composés).
L'arithmétique avec des variables de type comp, comme toute l'arithmétique SANE, est effectuée en interne en utilisant le type étendu pour l'arithmétique. Il n'y a aucune perte de précision, car la conversion de comp en extend est toujours exacte. Vous pouvez économiser de l'espace en entreposant les nombres dans le type comp, étant plus court qu'extended.
Valeurs représentées
Les types à virgule flottante (single, double et extended) entreposent les représentations binaires d'un signe (+ ou -), d'un exposant et d'une mantisse. Un nombre représenté a la valeur :
| ± mantisse * 2 exposant |
où pour les nombres normalisés, la mantisse a un seul bit à gauche du point binaire (c'est-à-dire 0 ≤ mantisse < 2).
Intervalle et précision des types SANE
L'intervalle et la précision des types réels pris en charge par SANE et MPW Pascal sont présentées dans le tableau précédent. Les intervalles décimales sont exprimées sous forme de représentations décimales hachées à deux chiffres des valeurs binaires exactes.
Exemples
En utilisant le type unique, le plus grand nombre représentable a :
| significatif | = 2 - 2-23 = 1.111111111111111111111112 |
|---|---|
| exposant | - 127 |
| valeur | = (2 - 2-23 ) * 2127 ≈ 3.403 * 1038 |
le plus petit nombre normalisé positif représentable a :
| significatif | = 1 = 1.000000000000000000000002 |
|---|---|
| exposant | = -126 |
| valeur | = 1 * 2-126 ≈ 1.175 * 10-38 |
et le plus petit nombre dénormalisé positif représentable a :
| significatif | = 2-23 = 0.000000000000000000000012 |
|---|---|
| exposant | = -126 |
| valeur | = 2-23 * 2-126 ≈ 1.401 * 10-45 |
Le type Single
Le format single 32 bits est divisé en trois champs, comme illustré dans l'image suivante :
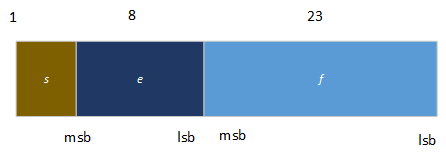
La valeur v du nombre est déterminée par ces champs :
- IF 0 < e < 255 THEN v = (-1)s * 2(e-127) * (1.∫)
- IF e = 0 and ∫ ≠ 0 THEN v = (-1)s * 2(-126) * (0.∫)
- IF e = 0 and ∫ = 0 THEN v = (-1)s * 0
- IF e = 255 and ∫= 0 THEN v = (-1)s * ∞
- IF e = 255 and ∫ ≠ 0 THEN v is a NaN
Le type Double
Un nombre double de 64 bits est divisé en trois champs :
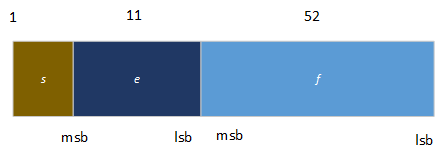
La valeur v du nombre est déterminée par ces champs :
- IF 0 < e < 2047 THEN v = (-1)s * 2(e-1023) * (1.∫).
- IF e = 0 AND ∫ ≠ 0 THEN v = (-1)s * 2(-1022) * (0.∫).
- IF e = 0 AND ∫ = 0 THEN v = (-1)s * 0.
- IF e = 2047 AND ∫ = 0 THEN v = (-1)s * ∞.
- IF e = 2047 AND ∫ ≠ 0 THEN v is a NaN.
Le type Comp
Un numéro de comp de 64 bits est divisé en deux champs :
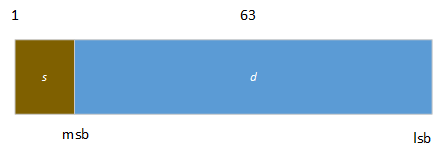
La valeur v du nombre est déterminée par ces champs :
- IF s=1 and d=0 THEN v est un unique comp NaN.
- OTHERWISE, v est la valeur complémentaire à 2 de la représentation 64 bits
Le type Extended
Un nombre de format extended de 80 bits est divisé en quatre champs :

La valeur v du nombre est déterminée par ces champs :
- IF 0 ≤ e &t; 32767 THEN v = (-1)s = 2(e-16383) * (i.∫)).
- IF e = 32767 and ∫ = 0 THEN v = (-1)s = ∞, outre le fait que i.
- IF e = 32767 and ∫ ≠ 0 THEN v is a NaN, outre le fait que i.
Le format étendu 96 bits utilisé lorsque -MC68881 est appelé ne diffère du format 80 bits que par l'inclusion de 16 bits d'espace inutilisé :

Arithmétique étendue
Alors que les types MPW Pascal single, double et comp sont destinés à un entreposage de données économique, le type étendu constitue la base de tous les calculs arithmétiques. Comme spécifié par la norme IEEE, toutes les opérations arithmétiques de base, y compris l'addition, la soustraction, la multiplication, la division et l'extraction de racine carrée, donnent les meilleurs résultats possibles. Dans MPW Pascal, ces opérations produisent des résultats étendus, ils sont donc précis avec une précision de 19 chiffres décimaux sur 2 intervalles dépassant 10-4900 à 10+4900.
Le MPW Pascal tire parti de l'arithmétique étendue en entreposant toutes les constantes numériques non entières au format étendu et en évaluant toutes les expressions numériques non entières en étendues, quels que soient les types impliqués. Par exemple, tout le côté droit de l'affectation ci-dessous sera calculé en étendu avant d'être converti dans le type du côté gauche :
Sans effort particulier de la part du programmeur, MPW Pascal effectue des calculs en utilisant la précision et la portée du type extended. Une précision supplémentaire signifie des erreurs d'arrondi plus petites afin que les résultats soient plus précis, plus souvent. Une portée supplémentaire signifie que les débordements et les sous-débordements sont moins fréquents, de sorte que les programmes fonctionnent plus souvent.
En suivant quelques pratiques de programmation simples, vous pouvez exploiter le type étendu au-delà de ce que MPW Pascal fait automatiquement pour vous.
Déclarez les variables utilisées pour les résultats intermédiaires comme étant de type étendu. Cette pratique est illustrée dans l'exemple suivant, calculant une somme de produits :
Si T avait été déclaré réel, comme les tableaux d'entrée X et Y et la somme des résultats, à chaque fois dans la boucle, l'affectation à T aurait provoqué une erreur d'arrondi à la limite de la simple précision. Dans l'exemple, toutes les erreurs d'arrondi sont à la limite de la précision extended, à l'exception de celle provoquée par l'affectation de T à la somme. Cela signifie que les erreurs d'arrondi seront moins susceptibles de s'accumuler pour produire un résultat inexact.
Déclarez les paramètres de valeur formelle et les résultats de fonction comme étant de type étendu, plutôt que Real, Double ou Comp. Cela évite à MPW Pascal d'avoir à effectuer des conversions inutiles entre les types numériques, ce qui peut entraîner une perte de précision. L'exemple ci-dessous illustre cette pratique.
Cas spéciaux
Bien que l'utilisation du type étendu fasse fonctionner les programmes plus souvent, des cas exceptionnels surviennent. Vos programmes peuvent contenir des instructions comme celles-ci :
- Average:=Sum/Count;
- Area:=Side*Side;
où toutes les variables sont de type Real. Que se passe-t-il si le nombre est nul, si le nombre et la somme sont tous deux nuls ou si le produit Side*Side est trop grand pour être représenté dans le format réel ?
Le MPW Pascal attribue des valeurs spéciales à Average et Area, et votre programme continue. En fait, la norme IEEE fait référence aux "exceptions" plutôt qu'aux "erreurs" et spécifie "pas d'arrêt" comme mode de fonctionnement par défaut pour son arithmétique. Si vous devez réinstaller les valeurs par défaut de l'IEEE, vous utiliserez cette instruction :
- SetEnvironment(IEEEDefaultEnv);
Notez que le type Environment n'est pas le type integer lorsque l'option -MC68881 est appelée, donc l'ancienne utilisation, SetEnvironment(0), ne fonctionnera plus avec cette option. Pour des raisons de compatibilité, SetEnvironment(IEEEDefaultEnv) fonctionne correctement quel que soit le paramètre de l'option -MC68881.
La bibliothèque SANE contient également des fonctions et des procédures permettant de déterminer quand des cas exceptionnels se produisent.
Classes de nombres
Les représentations dans les formats de données SANE se répartissent en cinq classes :
- Nombres normalisés - comme 3.0, 75.8, -2.3e78 et tous les autres pouvant être représentés par un bit de signification de 1.
- zéro -+0 et -0.
- Infinis - Infini positif et négatif
- NaNs - Abréviation de Not a Number.
- Nombres dénormalisés - nombres non nuls trop petits pour une représentation normalisée.
Infinis
Les infinis sont des représentations SANE spéciales pouvant survenir de deux manières à partir d'opérations sur des valeurs finies :
- Lorsqu'une opération doit produire un infini mathématique exact (comme 1/0), le résultat est un infini.
- Lorsqu'une opération produit un nombre dont l'ampleur est trop grande pour le format à virgule flottante prévu pour le nombre, le résultat peut (en fonction du sens d'arrondi actuel) être un infini.
MPW Pascal prédéfinit la constante inf pour avoir la valeur positive à l'infini. La constante de chaîne de caractères inf représente également l'infini pour l'entrée et la sortie de valeurs à virgule flottante. Les infinis se comportent comme des infinis mathématiques; par exemple, 1-inf =-inf. Les infinis peuvent être utiles même lorsque «l'arithmétique à l'infini» n'est pas l'objectif; par exemple, si x * x est trop grand pour le format étendu, l'expression 1+1/(X*X) calcule toujours la valeur correcte de un (en supposant que les arrêts de débordement sont désactivés).
Essaye ça :
NaN
Une autre représentation SANE spéciale est un NaN (Not a Number). Un NaN est produit chaque fois qu'une opération ne peut pas produire un résultat numérique significatif. Par exemple, 0/0 et Sqrt(-1) produisent des NaN.
Lorsqu'un NaN est généré par le logiciel SANE ou par des routines dans une bibliothèque SANE, un code NaN associé est renvoyé dans le cadre de la représentation du NaN. Ce code vous indique quel type d'opération a provoqué la création du NaN. Les codes NaN, présentés dans le tableau suivant, peuvent aider au débogage :
| Code | Description |
|---|---|
| 1 | Racine carrée non valide, telle que Sqrt(-1) |
| 2 | Ajout non valide, tel que (+inf) - (+inf) |
| 4 | Division invalide, telle que 0/0 |
| 8 | Multiplication non valide, telle que 0 * inf |
| 9 | Reste ou MOD non valide, tel que X MOD 0 |
| 17 | Tentative de conversion d'une chaîne ASSII non valide |
| 20 | Résultat de la conversion du comp NaN en format à virgule flottante |
| 21 | Tentative de création d'un NaN avec un code zéro |
| 33 | Paramètre invalide pour la routine de déclenchement |
| 34 | Paramètre invalide pour la routine de déclenchement inverse |
| 36 | Paramètre non valide pour enregistrer la routine |
| 37 | Paramètre non valide pour la routine xi ou xy |
| 38 | Paramètre invalide à la fonction financière |
Tous les NaN générés par le 68881 auront un code NaN de 255.
Important : Lorsque l'option -MC68881 est définie, de nombreux NaN du tableau précédent sont générés par le 68881; par conséquent, vous ne recevrez pas tous les paramètres répertoriés dans ce tableau.
L'instruction WriteLn(0/0) produira le résultat NAN(004) (à condition que l'arrêt de l'opération non valide soit désactivé). NAN(004), nan(4) et NaN sont des exemples d'entrées acceptables pour lire un NaN dans une variable SANE.
Nombres dénormalisés
Dans la mesure du possible, SANE entrepose les valeurs sous forme normalisée : le bit le plus significatif de la mantisse est un un plutôt qu'un zéro.
Cependant, lorsqu'un très petit nombre est entreposé et que l'exposant est la plus petite valeur négative possible, il est possible d'entreposer des valeurs encore plus petites en entreposant des zéros non significatifs. Par exemple :
- 1.0..02 * 2-126 - le plus petit réel normalisé
- 0.1..02 * 2-126- réel dénormalisé encore plus petit
En raison des nombres dénormalisés, l'arithmétique IEEE a la propriété souhaitable que a <> b si et seulement si a - b <> 0. Dans la plupart des arithmétiques non IEEE, a - b "rentrera à zéro" si a - b est trop petit, pour une représentation normalisée, même si a et b peuvent avoir des valeurs différentes.
Conditions exceptionnelles
Des conditions exceptionnelles peuvent résulter des calculs en virgule flottante dans un certain nombre de cas. Par exemple, la multiplication de deux valeurs très grandes peut entraîner une valeur trop grande pour être représentée dans l'un des formats de données MPW Pascal. Ou une opération telle que 0/0 peut être effectuée.
Le SANE permet à un programme de déterminer quand un calcul en virgule flottante a abouti à l'une de ces conditions exceptionnelles. Les conditions exceptionnelles se répartissent en cinq catégories :
- opération invalide
- sous-débordement
- débordement
- diviser par zéro
- inexact
Opération invalide
L'exception d'opération non valide survient lorsque les opérandes d'une opération ne sont pas valides, de sorte qu'un résultat numérique significatif est impossible. Par exemple, 0/0 et Sqrt(-1) sont des opérations non valides.
Sous-débordement
Un sous-débit se produit lorsqu'un résultat est à la fois dénormalisé et a perdu des chiffres significatifs en raison de l'arrondi. Par exemple, pour renvoyer le résultat de :
| (1.000000000000000000000012 * 2-126) / 2 |
au format réel, un zéro non significatif serait introduit et le dernier bit significatif serait perdu lors de l'arrondi. Le résultat :
| 0.10000000000000000000000002 * 2126 |
serait restitué et le sous-débordement serait signalé
Débordement
Un débordement se produit lorsqu'une valeur calculée est trop grande pour tenir dans le format de son type désigné. Le format de destination doit être l'un des types à virgule flottante ; si le format de destination est un type entier, l'exception non valide se produit.
Division par zéro
L'exception de division par zéro se produit lorsqu'un nombre fini non nul est divisé par zéro. Cela se produit également lorsqu'une opération sur des opérandes finis produit un résultat infini exact. Par exemple, l'opération 1/0 (aboutissant à INF) et l'opération Ln(0) (qui aboutit à -INF) signalent toutes deux une division par zéro.
Inexact
L'exception inexacte se produit lorsque le résultat arrondi d'une opération n'est pas identique au résultat mathématique (exact). (Ainsi, chaque fois qu'un dépassement ou un dépassement inférieur se produit, l'exception inexacte est signalée.) Par exemple, l'opération 2/3 signale une erreur inexacte, quel que soit le format à virgule flottante utilisé.
L'environnement SANE
L'«environnement» SANE est constitué de :
- Direction d'arrondissement
- Précision d'arrondissement
- Indicateurs d'exception
- Paramètres d'arrêt
La bibliothèque SANE comprend des procédures et des fonctions permettant de déterminer l'état actuel de l'environnement. Ces procédures et fonctions peuvent être utilisées pour signaler des conditions exceptionnelles et pour contrôler les paramètres d'environnement facultatifs. Par exemple, vous travaillez peut-être avec de très petites valeurs et avez besoin de savoir exactement quand un dépassement inférieur se produit. Ou vous souhaiterez peut-être que les conversions en virgule flottante soient arrondies à la baisse.
Les interfaces et bibliothèques SANE
Cette section explique chacune des constantes, types, fonctions et procédures contenus dans les interfaces et bibliothèques SANE. La bibliothèque SANELib881.o contient les mêmes procédures et fonctions disponibles dans SANELib.o mais doit être utilisée lorsque vous avez appelé l'option du compilateur -MC68881. La plupart du code SANE réel se trouve dans Pack4 et Pack5. SANELib.o et SANELib881.o contiennent des interfaces de code avec Pack4 et Pack5. Le fichier SANE.p contient le texte d'interface pour SANE.
Descriptions des constantes et des types
Chacune des constantes et des types définis par l'interface SANE est brièvement abordée dans la section suivante. Pour plus d'informations, consultez les descriptions des procédures et fonctions spécifiques mentionnées.
La constante DecStrLen
DecStrLen (longueur de chaîne de caractères décimale) est défini par :
- DecStrLen = 255;
DecStrLen est la constante définissant la longueur maximale d'une chaîne numérique décimale. C'est l'attribut size des variables de type DecStr.
Constantes de condition d'exception
Les déclarations définissant les cinq constantes de condition d'exception utilisées lorsque vous n'avez pas appelé l'option -MC68881 sont :
- Const
- Invalid=1;
- Underflow=2;
- Overflow=4;
- DivByZero=8;
- Inexact=16;
Ces constantes permettent de définir la valeur d'une variable de type Exception.
Par exemple, si e est une variable de type Exception, alors :
- e:=Invalid+Overflow+DivByZero;
donne une valeur représentant ces trois exceptions collectivement.
Les routines SetException, TestException, SetHalt et TestHalt acceptent toutes des arguments de type Exception.
Les déclarations définissant les 13 constantes de condition d'exception utilisées lorsque vous avez appelé l'option -MC68881 sont :
- Const
- Inexact=8;
- DivByZero=16;
- Underflow=32;
- Overflow=64;
- Invalid=128;
- CurInex1=256;
- CurInex2=512;
- CurDivByZero=1024;
- CurUnderflow=2048;
- CurOverflow=4096;
- CurOpError=8192;
- CurSigNaN=16384;
- CurBSonUnor=32768;
Reportez-vous au manuel d'utilisation du coprocesseur à virgule flottante MC68881 pour plus d'informations sur les exceptions 68881.
Le type DecStr
La déclaration définissant le type DecStr est :
- DecStr = STRING[DecStrLen];
Le type DecStr est une chaîne de caractères avec un attribut size de DecStrLen, soit 255 caractères. Il est utilisé pour contenir la représentation décimale, en caractères ASCII, d'un nombre.
Le type d'enregistrement DecForm
Un enregistrement de type DecForm (Decimal Format) est défini par cette déclaration :
Un enregistrement DecForm contient les spécifications du format d'un nombre décimal.
- Le champ Style détermine si la représentation décimale sera à virgule flottante ou à virgule fixe.
- Le champ Digits contient le nombre de chiffres significatifs pour le style flottant ou le nombre de chiffres à droite de la virgule décimale pour le style fixe.
La procédure Num2Str prend un argument DecForm. Elle utilise les informations de DecForm pour déterminer le format de la chaîne de caractères à renvoyer.
Le type RelOp
Le type RelOp (Relational Operator) est défini par :
- RelOp = (GreaterThan, LessThan, EqualTo, Unordered);
Un résultat de ce type est renvoyé par la fonction Relation, décrite plus loin.
Le type NumClass
Le type NumClass est défini par :
- NumClass = (SNaN, QNaN, Infinite, ZeroNum, NormalNum, DenormalNum);
Descriptions des classes de nombres :
| Classe de nombres | Descriptions |
|---|---|
| SNaN | Signalisation NaN |
| QNaN | NaN silencieux |
| Infinite | Infini ou -Infini |
| ZeroNum | 0 ou -0 |
| NormalNum | Nombre normalisé |
| DenormalNum | Numéro dénormalisé |
Les NaN silencieux sont le type habituel produit par les opérations à virgule flottante. Les NaN de signalisation, potentiellement utiles pour signaler les variables non initialisées, sont abordés dans le manuel Apple Numerics.
Le type NumClass est utilisé pour renvoyer les résultats des fonctions d'interrogation, décrites ci-dessous.
Le type Exception
Une variable de type Exception contient une valeur entière correspondant à la valeur de l'une des constantes Exception ou à une somme de deux ou plusieurs constantes Exception. Sauf si l'option -MC68881 est définie, le type d'exception est défini par :
- Exception=Integer;
Si l'option -MC68881 est définie, le type d'exception est défini par :
- Exception=LongInt;
Les routines SetException, TestException, SetHalt et TestHalt acceptent toutes des paramètres de type Exception.
Le type RoundDir
Le type RoundDir (Rounding Direction) est défini par :
- RoundDir = (ToNearest, Upward, Downward, TowardZero);
Le type RoundDir est utilisé pour déterminer comment les valeurs doivent être arrondies, lorsque l'arrondi devient nécessaire lors d'opérations arithmétiques ou de conversions. La procédure SetRound prend un paramètre de type RoundDir. La fonction GetRound renvoie une valeur de type RoundDir.
Le type RoundPre
Le type RoundPre (Rounding Precision) est défini par :
- RoundPre=(ExtPrecision, DblPrecision, RealPrecision);
La précision d'arrondi peut être utilisée pour simuler l'arithmétique avec une précision simple ou double uniquement. La procédure SetPrecision prend un argument de type RoundPre. La fonction GetPrecision renvoie une valeur de type RoundPre.
Le type Environment
Une variable de type Environment contient une valeur représentant les paramètres de l'environnement SANE. Par exemple, un paramètre IEEEDefaultEnv représente le paramètre IEEE par défaut (arrondi au plus proche, arrondi à précision étendue, exceptions supprimées et aucun arrêt défini). Sauf si l'option -MC68881 est définie, le type Environment est défini par :
- Environment=Integer;
Vous utilisez une variable de type Environment avec les routines d'accès à l'environnement SetEnvironment, GetEnvironment, ProcEntry et ProcExit.
Si -MC68881 est défini, le type Environment est défini par :
où PPCR représente le registre de contrôle à virgule flottante 68881 et FPSR représente son registre d'état à virgule flottante.
Procédures et fonctions numériques
Cette section comprend une description de chacune des procédures et fonctions des bibliothèques SANE. Des informations plus détaillées sont disponibles dans le manuel Apple Numerics.
N'oubliez pas que toute fonction avec un paramètre formel de l'un des types réels peut recevoir une valeur de n'importe quel type réel ou entier. Point flottant. Les paramètres de valeur dans MPW Pascal accepteront les expressions et les variables de l'un des types suivants : Integer, LongInt, Real (Single), Double, Comp ou Extended. Nous abrégeons la liste avec le terme argument numérique dans le texte explicatif ci-dessous.
Conversions entre types binaires numériques
Les bibliothèques SANE contiennent des fonctions convertissant les valeurs numériques (en représentation binaire) aux formats binaires des types Integer, LongInt et Extended.
Les fonctions Num2Integer et Num2LongInt
|
Function Num2Integer(X:Extended):Integer; Function Num2LongInt(X:Extended):LongInt; |
La fonction Num2Integer prend un paramètre numérique et renvoie un résultat de type Integer. La fonction Num2Longint prend un paramètre numérique et renvoie un résultat de type LongInt. La valeur renvoyée par ces fonctions dépend du sens d'arrondi (défini à l'aide de la procédure SetRound). En utilisant la direction d'arrondi standard, ToNearest, les exemples :
- Num2Integer(99.6);
- Num2LongInt(99.6);
renvoie la valeur 100,0.
Les Num2Integer et Num2LongInt sont similaires aux fonctions Round et Trunc de MPW Pascal. Cependant, Num2Integer et Num2LongInt prennent en compte le sens d'arrondi actuel. La fonction Round renvoie toujours la valeur du LongInt la plus proche ; la fonction Trunc arrondit toujours vers zéro.
Voici un exemple de la façon dont ces fonctions sont utilisées :
Une fois ce code exécuté, B et C ont tous deux la valeur 100 et D a la valeur 99.
Avec ce code, cependant, les valeurs de B et D sont 99. Mais la valeur de C est à nouveau 100. Les fonctions Round et Trunc calculent toujours leur valeur de la même manière, quel que soit le sens de l'arrondi.
En utilisant le sens d'arrondi ToNearest, Num2Integer et Num2Longint arrondissent les valeurs à mi-chemin entre deux entiers à l'entier pair le plus proche (comme prescrit par la norme IEEE). Par exemple, Num2Integer(2.5) renvoie deux. La fonction Round arrondit ces valeurs à mi-chemin de zéro. Par exemple, Round(2.5) renvoie trois.
La fonction Num2Extended
| Function Num2Extended(X:Extended):Extended; |
La fonction Num2Extended peut recevoir n'importe quel paramètre de type réel ou de type entier. Il convertit son paramètre au format Extended. Ceci est utile pour forcer l'arithmétique à virgule flottante lorsque toutes les variables impliquées sont de type entier.
Conversions entre chaînes de caractères décimales et binaires
La bibliothèque SANE comprend la procédure Num2Str et la fonction Str2Num pour convertir les nombres entre les représentations de caractères décimaux ASCII et binaires.
Remarque : Les procédures d'entrée et de sortie MPW Pascal utilisent les routines pour les conversions Pascal d'entrée/sortie entre ASCII décimal et binaire.
La procédure Num2Str
| Function Num2Str(f:DecForm;x:Extended;Var S:DecStr); |
La procédure Num2Str convertit une valeur numérique x en une chaîne de caractères décimale, renvoyée en s, en utilisant les spécifications de l'enregistrement DecForm f. Voici quelques exemples de la manière dont Num2Str utilise les paramètres lui étant passés pour former une chaîne de caractères :
| Dec:Form.Style | Dec:Form.Digits | x | S |
|---|---|---|---|
| FloatDecimal | 6 | 123.45 | ' 1.23450e+2' |
| FloatDecimal | 2 | 123.45 | ' 1.2e+2' |
| FixedDecimal | 6 | 123.45 | '123.450000' |
| FixedDecimal | 2 | 123.45 | '123.45' |
La fonction Str2Num
| Function Str2Num(S:DecStr):Extended; |
La fonction Str2Num prend un paramètre de chaîne de caractères décimal (de type DecStr) et le convertit en type Extended.
Fonctions arithmétiques, auxiliaires et élémentaires
La bibliothèque SANE comprend un ensemble de fonctions complétant les fonctions arithmétiques.
La fonction Remainder
| Function Remainder(x,y:Extended;Var quo:Integer); |
La fonction Remainder renvoie le reste de la division de ses deux paramètres numériques x/y, comme spécifié par la norme IEEE. Cette fonction renvoie un reste exact de la plus petite magnitude possible. Le résultat est calculé sous la forme x-n*y, où n est l'approximation intégrale la plus proche du quotient x/y. Par exemple, Remainder(9,5,q) renvoie -1, car -1*9-2*5.
Le paramètre de la variable entière quo reçoit les 7 bits de poids faible de n comme valeur comprise entre -127 et 127; ceci est utile pour programmer des fonctions, comme les fonctions trigonométriques, nécessitant une réduction de paramètres.
Remarque : N'oubliez pas que l'opérateur Pascal MOD ne peut être utilisé qu'avec des valeurs intégrales. La fonction Remainder peut être utilisée avec des valeurs de type réel ou entier.
La fonction Rint
| Function Rint(X:Extended):Extended; |
La fonction Rint prend un paramètre numérique et l'arrondit à une valeur entière au format étendu. Notez que toutes les valeurs à virgule flottante suffisamment grandes sont intégrales. Le résultat dépend du sens de l'arrondi, pouvant être modifié à l'aide de la procédure SetRound.
La fonction Scalb
| Function Scalb(n:Inteqer;X:Extended):Extended; |
La fonction Scalb prend deux paramètres. Le premier est une valeur de type entier ; la seconde est une valeur étendue. La fonction met à l'échelle la valeur Extended par la puissance de deux spécifiée par le paramètre Integer. La valeur 2nx est renvoyée au format Extended.
La fonction Logb
| Function Logb(X:Extended):Extended; |
La fonction Logb prend un paramètre numérique et renvoie la plus grande puissance de deux ne dépassant pas la grandeur de son paramètre. Par exemple, Logb(-65535) donne 15 car 215 ≤ 65535 < 216.
La fonction CopySign
| Function CopySign(X,Y:Extended):Extended; |
La fonction CopySign prend des paramètres numériques. Il renvoie une valeur égale au deuxième paramètre, mais avec le signe du premier paramètre. Par exemple, CopySign(2.0,-3.0) donne 3,0. La fonction CopySign renvoie une valeur Extended.
La fonction NextReal
| Function NextReal(x,y:Real):Extended; |
La fonction NextReal prend deux paramètres réels. Il renvoie la prochaine valeur pouvant être représentée au format réel après le premier paramètre, dans la direction du deuxième paramètre. Il renvoie une valeur Extended.
Remarque : Bien que NextReal, NextDouble et NextExtended puissent accepter n'importe quel paramètre numérique, NextReal convertit en interne ses paramètres en réel, NextDouble en double et NextExtended en étendu.
La fonction NextDouble
| Function NextDouble(X,Y:Double):Extended; |
La fonction NextDouble prend deux paramètres Double. Il renvoie la valeur suivante pouvant être représentée au format Double après le premier paramètre, dans la direction du deuxième paramètre. Il renvoie une valeur étendue.
La fonction NextExtended
| Function NextExtended(X,Y:Extended):Extended; |
La fonction NextExtended prend deux paramètres étendus. Il renvoie la valeur suivante pouvant être représentée au format étendu après le premier paramètre, dans la direction du deuxième paramètre. Il renvoie une valeur étendue.
La fonction Log2
| Function Log2(X:Extended):Extended; |
La fonction Log2 prend un paramètre numérique et renvoie le logarithme base 2 de son paramètre au format étendu.
La fonction Ln1
| Function Ln1(X:Extended):Extended; |
La fonction Ln1 prend un paramètre numérique et renvoie le logarithme base-e de un plus le paramètre : Ln(1+x). Il renvoie une valeur Extended. Pour x proche de zéro, Ln1(x) est plus précis que Ln(1.0+x).
La fonction Exp2
| Function Exp2(X:Extended):Extended; |
La fonction Exp2 prend un paramètre numérique et renvoie deux élevés à la puissance du paramètre : 2x. Il renvoie une valeur Extended.
La fonction Exp1
| Function Exp1(X:Extended):Extended; |
La fonction Exp1 prend un paramètre numérique et renvoie ex-1. Il renvoie une valeur Extended. Pour x proche de zéro, Exp1(X) est plus précis que Exp(x)-1.0.
La fonction XpwrI
| Function XpwrI(x:Extended;i:Integer):Extended; |
La fonction XpwrI prend un paramètre numérique et un paramètre entier. Il renvoie la valeur de son premier paramètre élevé à la puissance spécifiée par le paramètre Integer : xi. Il renvoie une valeur Extended.
La fonction XpwrY
| Function XpwrY(x,y:Extended):Extended; |
La fonction XpwrY prend deux paramètres numériques. Il renvoie la valeur du premier paramètre, élevée à la puissance spécifiée par le deuxième paramètre : xy. Il renvoie une valeur Extended.
Fonctions financières
Le SANE propose deux fonctions pouvant être utilisées dans les applications financières : la fonction composée et la fonction Annuity.
La fonction Compound
| Function Compound(r,n:Extended):Extended; |
La fonction Compound prend deux paramètres numériques. Le premier paramètre spécifie le taux d'intérêt ; la seconde précise le nombre de périodes composées. Il renvoie (1+r)n, correspondant au principal plus les intérêts composés courus sur un investissement initial d'une unité. Il renvoie une valeur Extended.
La fonction Annuity
| Function Annuity(r,n:Extended):Extended; |
La fonction Annuity prend deux paramètres numériques. Le premier paramètre spécifie le taux d'intérêt ; la seconde précise le nombre de périodes. La rente renvoie (1-(1+r)-n)/r, étant le facteur de valeur actuelle d'une rente ordinaire. Il renvoie une valeur étendue. Voici un exemple de la façon dont la fonction Rente peut être utilisée :
- Program _Loan;
-
- Uses SANE;
-
- Var
- Loan,Payment,Interest,Periods:Extended;
-
- BEGIN
- WriteLn('Montant du prêt: ');
- ReadLn(Loan);
- Writeln('Taux d''intérêt annuel (Entrez sous forme décimale.) :');
- ReadLn(Interest);
- WriteLn('Nombre d''années:');
- ReadLn(Periods);
- Payment:= Loan/Annuity(Interest/12,Periods*12);
- Write('Votre paiement est : ');
- Write(Payment:8:2);
- END.
Dans cet exemple, étant donné un montant de prêt de 120 000 $ et un taux d'intérêt de 0,1075 sur 30 ans, le paiement mensuel sera de 1 120,18 $.
Fonctions trigonométriques
Le MPW Pascal inclut les fonctions prédéfinies Sin, Cos et Arctan. De plus, la bibliothèque SANE fournit la fonction Tan.
La fonction Tan
| Function Tan(X:Extended):Extended; |
La fonction Tan renvoie la tangente d'un paramètre numérique. Notez que le paramètre doit être exprimé en radians. La fonction Tan renvoie une valeur Extended.
Routines transcendantales supplémentaires
Le MPW Pascal prédéfinit ces neuf routines lorsque l'option -MC68881 du compilateur est utilisée. Ces routines ne font pas partie de l'interface SANE et sont indisponibles sans l'option -MC68881.
La fonction Arctanh
| Function Arctanh(X:Extended):Extended; |
La fonction Arctanh renvoie l'arctangente hyperbolique d'un paramètre numérique. La fonction Arctanh renvoie une valeur étendue.
La fonction Cosh
| Function Cosh(X:Extended):Extended; |
La fonction Cosh renvoie le cosinus hyperbolique d'un paramètre numérique. La fonction Cosh renvoie une valeur Extended.
La fonction Sinh
| Function Sinh(X:Extended):Extended; |
La fonction Sinh renvoie le sinus hyperbolique d'un paramètre numérique. La fonction Sinh renvoie une valeur Extended.
La fonction Tanh
| Function Tanh(X:Extended):Extended; |
La fonction Tanh renvoie la tangente hyperbolique d'un paramètre numérique. La fonction Tanh renvoie une valeur Extended.
La fonction Log10
| Function Log10(X:Extended):Extended; |
La fonction Log10 renvoie le logarithme base 10 d'un paramètre numérique. La fonction Log10 renvoie une valeur Extended.
La fonction Exp10
| Function Exp10(X:Extended):Extended; |
La fonction Exp10 renvoie dix élevé à la puissance d'un paramètre numérique : 10x. La fonction Exp10 renvoie une valeur Extended.
La fonction Arccos
| Function Arccos(X:Extended):Extended; |
La fonction Arccos renvoie la valeur principale, en radians, de l'arccosinus d'un paramètre numérique. La fonction Arccos renvoie une valeur Extended.
La fonction ArcSin
| Function Arcsin(X:Extended):Extended; |
La fonction Arcsin renvoie la valeur principale, en radians, de l'arc sinus d'un paramètre numérique. La fonction Arcsin renvoie une valeur Extended.
La procédure SinCos
| Procedure SinCos(Var S,C:Extended;X:Extended); |
La procédure SinCos définit simultanément la variable S sur Sin(X) et la variable C à Cos(X). Le paramètre X est un paramètre numérique. La procédure SinCos est plus rapide que les appels de fonctions séparés à Sin et Cos.
Fonctions d'enquête
Le SANE comprend plusieurs fonctions vous permettant de déterminer la classe d'une valeur numérique. Le résultat de chacune de ces fonctions est du type NumClass, décrit ci-dessus. De plus, ils incluent une fonction renvoyant le signe d'un paramètre numérique.
La fonction ClassReal
| Function ClassReal(Var X:Extended):NumClass; |
La fonction ClassReal détermine la classe numérique d'un paramètre numérique comme si le paramètre était converti au format Real. Par exemple :
Le premier appel de fonction renvoie NormalNum, le code d'un nombre normalisé. Le deuxième appel renvoie ZeroNum, le code de zéro (car 1e-310 arrondit à +0 dans le format Real).
La fonction ClassDouble
| Function ClassDouble(X:Double):NumClass; |
La fonction ClassDouble détermine la classe numérique d'un paramètre numérique comme si le paramètre était converti en un format double. Le résultat est de type NumClass. Par exemple :
Le premier exemple renvoie QNaN, le code d'un NaN silencieux. Le deuxième exemple renvoie DenormalNum, le code d'un nombre dénormalisé (car 1e-310 est dénormalisé au format double).
La fonction ClassExtended
| Function ClassExtended(X:Extended):NumClass; |
La fonction ClassExtended détermine la classe numérique d'un paramètre numérique comme si le paramètre était converti dans un format étendu. Le résultat est de type NumClass. Par exemple :
Le premier exemple renvoie Infinite, le code des infinis. Le deuxième exemple renvoie NormalNum, le code d'un nombre normalisé.
La fonction ClassComp
| Function ClassComp(x:Comp):NumClass; |
La fonction ClassComp détermine la classe numérique de son paramètre numérique comme si le paramètre était converti au format comp. Le résultat est de type NumClass. Par exemple :
Le premier exemple renvoie NormalNum, le code d'un nombre normal. Le deuxième exemple renvoie zeroNum, le code de zéro. (N'oubliez pas que comp entrepose les valeurs intégrales.)
La fonction SigNum
| Function SignNum(x:Extended):Integer; |
La fonction SignNum prend un paramètre numérique et renvoie une valeur entière indiquant le signe du paramètre. La valeur renvoyée est un si le signe du paramètre est négatif, zéro si le signe du paramètre est positif.
La fonction RandomX
| Function RandomX(Var x:Extended):Extended; |
La fonction RandomX prend un paramètre variable de type Extended devant contenir une valeur intégrale comprise entre 1 ≤ x ≤ 231-2. Il renvoie le nombre aléatoire suivant (au format étendu) en séquence dans le même intervalle. Le paramètre variable est mis à jour avec la valeur renvoyée. RandomX utilise cet algorithme :
| NewX = (75*OldX) MOD (231-1) |
La fonction NaN
| Function Nan(x:Integer):Extended; |
La fonction Nan prend un paramètre entier et renvoie un NaN, au format étendu, associé au code donné en paramètre.
La fonction Relation
| Function Relation(x,y:Extended):RelOp; |
La fonction Relation prend deux paramètres numériques et renvoie une valeur de type Relop. La valeur renvoyée spécifie la relation entre les deux paramètres. Par exemple, Relation(0,1,NaN(0)) renvoie un ordre non ordonné, car toutes les comparaisons impliquant des NaN sont non ordonnées. La relation (1, 3, 9) renvoie LessThan.
Procédures et fonctions d'accès à l'environnement
Les routines d'accès environnemental SANE vous permettent de déterminer comment les calculs doivent être effectués et comment répondre à des conditions exceptionnelles. L'environnement est constitué de :
- Le sens de l'arrondi
- La précision de l'arrondi
- Indicateurs d'exception
- Arrêter les paramètres
Le sens de l'arrondissement
Le sens de l'arrondi peut être défini de quatre manières :
- ToNearest
- Upward
- Downward
- TowardZero
La direction d'arrondi par défaut est ToNearest. Vous pouvez découvrir quelle est la direction d'arrondi actuelle en utilisant la fonction GetRound. Vous pouvez modifier le sens de l'arrondi à l'aide de la procédure d'arrondi définie.
La fonction GetRound
| Function GetRound:RoundDir; |
La fonction GetRound renvoie la direction d'arrondi actuelle sous la forme d'une valeur de type RoundDir.
La procédure SetRound
| Procedure SetRound(r:RoundDir); |
La procédure SetRound prend un paramètre de type RoundDir. La procédure définit la direction d'arrondi effective sur celle indiquée par le paramètre. Par exemple, le code ci-dessous enregistre le sens d'arrondi actuel, calcule une fonction en utilisant l'arrondi TowardZero et restaure enfin le sens d'arrondi enregistré.
Précision d'arrondi
Vous souhaiterez peut-être utiliser SANE pour effectuer des calculs et simuler les résultats que vous obtiendriez si vous utilisiez un système ne fournissant pas d'arithmétique de précision étendue. Normalement, tous les calculs à virgule flottante MPW Pascal renvoient des résultats arrondis à une précision et un intervalle étendues. Cependant, la précision d'arrondi peut être réglée sur une précision et un intervalle simples ou doubles. Les résultats seront toujours renvoyés au format étendu. Il n'y a aucun avantage en termes de performances à définir une précision d'arrondi simple ou double. Vous pouvez accéder à la précision de l'arrondi à l'aide de la procédure SetPrecision et de la fonction GetPrecision.
La fonction GetPrecision
| Function GetPrecision:RoundPre; |
La fonction GetPrecision renvoie une valeur de type RoundPre, indiquant la précision d'arrondi actuelle.
La procédure SetPrecision
| Procedure SetPrecision(p:RoundPre); |
La procédure SetPrecision prend un paramètre étant une variable de type RoundPre, indiquant la précision d'arrondi souhaitée.
Des exceptions
Lorsque -MC68881 n'est pas défini, les résultats exceptionnels résultant de calculs numériques se répartissent en cinq catégories. Le fichier SANE.p dans PInterfaces définit une constante pour chaque type d'exception, comme indiqué dans le tableau suivant :
| Exception | Valeur de la constante | Description | Exemple |
|---|---|---|---|
| Invalid | 1 | Opération non significative - résultat NaN | Sqrt(-1) |
| Underflow | 2 | Précision perdue - résultat trop petit | 2-16383/3 |
| Overflow | 4 | Résultat trop grand pour la représentation numérique | 216384 |
| DivByZero | 8 | Division d'un nombre différent de zéro par zéro | 1/0 |
| Inexact | 16 | Le résultat arrondi n'est pas le même que le résultat mathématique exact | 1/3 |
Les exceptions indiquées dans le tableau précédent se produisent dans les conditions suivantes :
- Si une opération non valide est effectuée, Invalid est défini
- Si un sous-dépassement se produit, le Underflow (sous-dépassement) est défini.
- En cas de débordement, le Overflow (débordement) est défini.
- Si une division par zéro se produit, DivByZero est défini.
- Si le résultat du calcul est inexact, Inexact est défini.
Le tableau suivant répertorie les résultats exceptionnels pouvant se produire lorsque -MC68881 est défini. Le préfixe Cur représente l'exception actuelle. Ces huit valeurs correspondent à l'octet d'état d'exception 68881.
| Exception | Valeur constante |
|---|---|
| Inexact | 8 |
| DivByZero | 16 |
| Underflow | 32 |
| Overflow | 64 |
| Invalid | 128 |
| CurInex1 | 256 |
| CurInex2 | 512 |
| CurDivByZero | 1024 |
| CurUnderflow | 2048 |
| CurOverflow | 4096 |
| CurOpError | 8192 |
| CurSigNaN | 16384 |
| CurBSonUnor | 32768 |
La procédure SetException
| Procedure SetException(e:Exception;b:Boolean); |
La procédure SetException prend un paramètre de type Exception et un deuxième paramètre de type Boolean. Si le deuxième paramètre est vrai, la procédure signale les exceptions codées dans son premier paramètre. Si le deuxième paramètre est faux, il efface les indicateurs d'exception spécifiés par le premier paramètre. Par exemple :
- SetException(Overflow+Inexact,True);
signale les exceptions Overflow et Inexact. Si l'arrêt en cas de débordement ou Inexact était défini, cette instruction arrêterait le programme.
La fonction TestException
| Function TestException(e:Exception):Boolean; |
La fonction TestException prend un paramètre de type Exception et renvoie une valeur booléenne indiquant si l'une des exceptions codées dans son paramètre est définie ou non.
Suite à l'instruction SetException ci-dessus, l'instruction :
- TestException(OverFlow+Invalid);
reviendrait true.
Utiliser des conditions exceptionnelles pour arrêter un programme
L'environnement SANE inclut un paramètre d'arrêt pour chacune des exceptions déterminant si l'occurrence de l'exception arrête le programme. Par défaut, le MPW Pascal adhère à la norme IEEE en initialisant tous les arrêts à effacé (off).
Vous pouvez accéder aux paramètres d'arrêt à l'aide de la fonction TestHalt et de la procédure SetHalt.
La fonction TestHalt
| Function TestHalt(e:Exception):Boolean; |
La fonction TestHalt prend un paramètre de type Exception et renvoie une valeur booléenne. Si l'un des arrêts indiqués par le paramètre Exception est défini, la fonction renvoie true ; sinon, il renvoie false.
La procédure SetHalt
| Procedure SetHalt(e:Exception;b:Boolean); |
La procédure SetHalt prend deux paramètres. Le premier est de type Exception. Cela indique les exceptions pour lesquelles vous souhaitez arrêter votre programme. Le deuxième paramètre est de type Boolean. Si la valeur du paramètre Boolean est true, les occurrences des exceptions indiquées entraîneront l'arrêt de votre programme. Si c'est False, votre programme continuera à s'exécuter lorsque ces exceptions se produiront.
Arrêts et le 68881
Lorsque l'option -MC68881 est définie, les arrêts en virgule flottante sont générés par le 68881 et non par Pack4. Les anciennes sources d'un gestionnaire d'arrêt ne fonctionneront plus lorsqu'elles seront compilées avec l'ensemble -MC68881.
Pour plus de détails sur les gestionnaires d'arrêt SANE compatibles avec Pack4. La prise en charge suivante pour 68881 arrêts et interruptions a été ajoutée au fichier SANE.p :
- Type
- TrapVector=Record
- Unordered:LongInt;
- Inexact:LongInt;
- DivByZero:LongInt;
- Underflow:LongInt;
- OpError:LongInt;
- Overflow:LongInt;
- SigNaN:LongInt;
- End;
-
- Procedure GetTrapVector(Var Traps:TrapVector); { Pièges <-- vecteurs de pièges FPCP }
- Procedure SetTrapVector(Traps: TrapVector); { Vecteurs de pièges FPCP <-- Pièges }
La définition du type TrapVector et ses procédures associées, GetTrapVector et setTrapVector, vous donnent accès à ces vecteurs d'exceptions 68020 gérant les exceptions 68881 à virgule flottante. Les procédures permettant de définir et d'obtenir des arrêts, des exceptions et des environnements fonctionnent comme lorsque -MC68881 n'est pas défini ; ils ne diffèrent que par les types de données utilisés comme paramètres.
Enfin, contrairement au mécanisme d'arrêt Pack4, le 68881 prend en charge le mécanisme de piège recommandé par l'IEEE. Le mot piège apparaît dans les noms ci-dessus pour souligner cette différence. Les pièges IEEE faussent parfois l'exposant des résultats à virgule flottante ; dans certains cas, les exceptions sont définies différemment lorsque les interruptions sont activées, et la pile transmise à un gestionnaire d'interruptions est configurée différemment par le mécanisme d'interruption 68881.
Sauvegarde et restauration des paramètres d'environnement
L'ensemble de l'environnement SANE (direction d'arrondi, précision d'arrondi, indicateurs d'exception et paramètres d'arrêt) peut être codé dans une valeur de type Environment. Les procédures décrites ci-dessous accèdent à l'environnement SANE actuel dans son ensemble. Ils sont utiles pour gérer l'environnement afin que les routines s'exécutent avec les environnements dont elles ont besoin et pour contrôler les informations d'exception transmises entre les routines.
La procédure GetEnvironment
| Procedure GetEnvironment(Var e:Environment); |
La procédure GetEnvironment prend un paramètre de type Environment comme paramètre de variable et affecte les paramètres actuels de l'environnement à cette variable.
Lorsque votre programme démarre, l'environnement reflétera les valeurs par défaut de MPW Pascal :
- Direction d'arrondi ToNearest
- Précision d'arrondi Extended
- Tous les indicateurs d'exception ont été effacés.
- Aucun arrêt défini
La procédure SetEnvironment
| Procedure SetEnvironment(e:Environment); |
La procédure SetEnvironment prend un paramètre de type Environment. Il définit l'environnement à virgule flottante sur celui codé dans son paramètre. Pour réinstaller l'environnement par défaut, utilisez l'instruction :
- SetEnvironment(IEEEDefaultEnv);
La procédure suivante garantit qu'il s'exécutera dans l'environnement par défaut IEEE, sans affecter l'environnement de son appelant :
Notez que le type Environment n'est pas le type entier lorsque l'option -MC68881 du compilateur est appelée, donc l'ancienne utilisation, SetEnvironment(0), ne fonctionnera plus avec cette option. Pour des raisons de compatibilité, SetEnvironment(IEEEDefaultEnv) fonctionne correctement quel que soit le paramètre de l'option -MC68881.
La procédure ProcEntry
| Procedure ProcEntry(Var e:Environment); |
La procédure ProcEntry enregistre l'environnement actuel (la direction de l'arrondi, la précision de l'arrondi, les indicateurs d'exception et les paramètres d'arrêt) dans la variable d'environnement transmise à la procédure, puis définit l'environnement sur les valeurs par défaut IEEE. L'instruction ProcEntry(e) est équivalente à :
- GetEnvironment(e);
- SetEnvironment(IEEEDefaultEnv);
La procédure ProcExit
| Procedure ProcExit(e:Environment); |
La procédure ProcExit prend un paramètre de type Environment. Il enregistre temporairement les indicateurs d'exception actuels, définit l'environnement effectif comme étant celui codé dans son paramètre, puis signale les exceptions temporairement enregistrées.
ProcEntry et ProcExit peuvent être utilisés dans des routines pour masquer sélectivement les exceptions suspectes des appels de la routine. Par exemple :
ProcEntry(e) enregistre l'environnement de l'appelant dans e et définit les valeurs par défaut IEEE afin que les exceptions ne puissent pas interrompre la routine. Si x = -1, le calcul du côté droit de l'affectation à ArcCos signalera DivByZero, même si ArcCos se verra attribuer la valeur correcte, PI. SetException(DivByZero,False) efface l'indicateur DivByZero afin que l'appelant ne le voie jamais. Si x > 1 ou x < -1, le calcul d'Arccos signalera de manière appropriée Invalid. La procédure ProcExit renverra Invalid après la restauration de l'environnement de l'appelant, donc si l'environnement de l'appelant demande des arrêts sur invalide, l'arrêt se produira.
Prise en charge du 68881
La liste suivante résume la prise en charge de MPW Pascal pour le coprocesseur à virgule flottante 68881. Des informations détaillées sur SANE et la programmation du 68881 sont fournies dans les sections ci-dessous.
- Les applications compilées sans l'option -MC68881 s'exécuteront sur tous les Macintosh. Si -MC68881 est défini, votre application s'exécutera uniquement avec un 68020 et un 68881 sur l'ordinateur.
- Une bibliothèque, SANELib881.o, a été ajoutée et le fichier d'interface SANE.p a été mis à jour pour fournir la prise en charge du coprocesseur à virgule flottante.
- L'option de ligne de commande -MC68881 peut être utilisée pour accéder directement au 68881 pour l'addition, la soustraction, la multiplication, la division, la racine carrée, le reste, la conversion binaire-binaire et la comparaison. Lorsque cette option est définie, vous devez établir une liaison avec SANELib881.o au lieu de SANELib.o.
- Pour le même effet, vous pouvez taper {$MC68881+} dans le code source (il doit apparaître au début du fichier avant toute déclaration VAR, PROCEDURE ou FUNCTION ou toute instruction USES).
- Avec l'option -MC68881, le type Extended devient long de 12 octets et les variables de type Extended peuvent être allouées aux registres.
- Par défaut, le compilateur appelle Packs pour exécuter des fonctions transcendantales (élémentaires) précises et entièrement compatibles même si vous avez défini l'option -MC68881.
- Si vous souhaitez que le compilateur émette des appels au 68881 pour des fonctions transcendantales entièrement compatibles, mais très rapides, alors ajoutez -d Elems881=true à la ligne de commande Pascal.
SANE et le 68881
Le SANE est l'environnement numérique d'Apple. Il s'agit d'un surensemble de valeurs numériques de la norme IEEE 754. Tous les ordinateurs Apple et la plupart des langages de programmation Apple intègrent SANE. Dans la famille Macintosh, SANE est contenu dans la ROM système sous forme de Pack4 et de Pack5. Le MPW Pascal gère l'arithmétique à virgule flottante en émettant du code pour appeler les Packs. La virgule flottante dans la famille Macintosh est identique en termes de précision et, à l'exception du Macintosh II, à peu près aussi rapide.
Les performances en virgule flottante sur le Macintosh II sont d'un ordre de grandeur plus rapides que sur le Macintosh Plus car Pack4 et Pack5 (dans la ROM du Macintosh II) tirent parti du coprocesseur à virgule flottante 68881 chaque fois que cela est possible. Le 68881 est une puce à virgule flottante très rapide, entièrement conforme à la norme IEEE 754 et, comme SANE, possède plusieurs extensions intégrées à la norme IEEE. Pour les performances en virgule flottante les plus rapides possibles, MPW Pascal peut utiliser directement le 68881, évitant ainsi les appels à Pack4 et Pack5.
L'option de ligne de commande -MC68881 indique au compilateur d'utiliser les appels 68881 pour les opérations arithmétiques de base (addition, soustraction, multiplication, racine carrée, reste, comparaison et conversions de format binaire-binaire). Lorsque vous invoquez cette option, les trois effets suivants se produisent :
- La taille du type de données Extended change.
- L'arithmétique s'exécute environ deux ordres de grandeur plus rapidement que sur Macintosh Plus (environ un ordre de grandeur plus rapide que sur Macintosh II sans l'option -MC68881).
- Votre application contiendra des instructions 68881 et ne fonctionnera donc plus sur un Macintosh sans 68881.
Les valeurs des résultats seront identiques à celles reçues sans l'option -MC68881. Une autre option, écrite -d Elems88l=true, demande au compilateur d'utiliser les appels 68881 pour toutes les 68881 fonctions transcendantales (logarithmes, exponentielles, trigonométriques et trigonométriques hyperboliques). Cette option n'a aucune signification sauf si l'option -MC68881 est déjà appelée ; de plus, il a deux effets importants :
- Les résultats seront différents des résultats sans l'option -d Elems881=true car Pack5 en ROM est plus précis dans ses fonctions transcendantales que le 68881.
- La performance des fonctions transcendantales s'améliorera de plus d'un autre ordre de grandeur.
En savoir plus sur le 68881
Le Pascal vous permet de redéfinir toutes les fonctions, procédures et types prédéfinis. L'utilisation de -d Elems881=true, décrite ci-dessus, contrôle simplement la redéfinition de plusieurs routines intégrées au compilateur. SANE.p dans le dossier PInterfaces contient des déclarations de 19 fonctions transcendantales prédéfinies par le compilateur. Les fonctions transcendantales se répartissent en trois groupes :
- Fonctions prédéfinies en Pascal, notamment Sin, Cos, Arctan, Exp et Ln.
- Fonctions SANE, notamment Tan, Exp1, Exp2, Ln1 et Log2.
- Fonctions supplémentaires, notamment Arctanh, Cosh, Sinh, Tanh, Log10, Exp10, Arccos, Arcsin et Sincos.
Lorsque -d Elems881=-true est défini (et que -MC68881 est invoqué), le compilateur effectue des appels directs 68881 pour toutes les fonctions prédéfinies Pascal, les fonctions SANE et les fonctions supplémentaires répertoriées ci-dessus. Sinon, les déclarations des fonctions prédéfinies Pascal et des fonctions SANE sont vues par le compilateur dans SANE.p, les appels directs à ces fonctions ne sont pas effectués et le compilateur génère des appels aux versions de ces routines trouvées dans SANELib881.o. En effet, SANE.p indique au compilateur d'appeler la version de ces fonctions ainsi, est fourni au moment du lien dans le fichier SANELib881.o du dossier {Plibraries}. SANELib881.o, à son tour, appelle les Pack5 dans la ROM pour plus de précision et de compatibilité. (Lorsque l'option -MC68881 est définie, il crée un lien uniquement avec SANELib881.o ; sinon, il crée un lien avec SANELib.o.)
Usage des registres
Le 68881 ajoute huit nouveaux registres, appelés FP0,...,FP7, aux familiers D0,...,D7 et A0,...,A7 du 68020. Les registres FP ont une largeur de 96 bits et sont conçus pour contenir données de précision étendue. Le Pascal optimise l'utilisation de ces registres pour les variables et pour l'évaluation des expressions. Le Pascal place les variables dans FP4, ..., FP7 et alloue FP0, ..., FP3 comme registres de travail.
Par exemple, toutes les expressions à virgule flottante, telles que le côté droit de :
- x:=3*y+6;
sont évalués dans les registres FP. Si x et y sont des variables de type étendu, le compilateur peut également les allouer à des registres, améliorant encore davantage les performances.
Conversion entre formats Extended dans les programmes à monde mixte
Apple recommande de compiler tous vos fichiers programme soit avec l'option -MC68881 jamais définie, soit avec cette option toujours définie. La construction d'un programme avec des paramètres mixtes de cette option provoque des problèmes des manières suivantes :
- Les constantes et variables Extended dans certaines parties d'un programme à paramètres mixtes ont une longueur de 80 bits; dans d'autres parties, ils font 96 bits. Cela peut poser des problèmes lorsqu'une partie de votre programme fait référence à des constantes et des variables d'une autre partie avec l'autre format Extended.
- Étant donné que les paramètres de valeur à virgule flottante sont toujours promus au format étendu, l'appel d'une fonction ayant l'autre format étendu peut provoquer des problèmes.
- Les deux bibliothèques SANE SANELib.o et SANELib881.o contiennent des routines portant des noms identiques. Pour faire référence aux routines des deux bibliothèques dans la même étape de liaison :
- Utilisez Lib pour créer votre propre bibliothèque (en sélectionnant les routines dont vous avez besoin dans l'une des bibliothèques).
- Renommez les routines et les modules les contenant pour éviter les collisions de noms. Ceci est encore compliqué par l'utilisation de DumpObj pour déterminer les noms des modules contenant les points d'entrée dont les noms doivent être modifiés.
- Lien avec votre nouvelle bibliothèque et avec la bibliothèque SANE inchangée.
Si vous devez mélanger des fichiers contenant différents formats étendus, une prise en charge limitée est proposée pour résoudre le problème lié à l'appel d'une fonction possédant l'autre format étendu. SANE.p définit les fonctions suivantes pour convertir entre les formats étendus 96 bits et 80 bits :
|
Function X96to80(X:Extended96):Extended; Function X80to96(X:Extended):Extended96; |
pour une utilisation dans le monde 80 bits, et :
|
Function X96to80(X:Extended):Extended80; Function X80to96(X:Extended80):Extended96; |
pour une utilisation dans le monde 96 bits.
Les types :
et :
ne sont utiles que dans ces routines de transfert - vous ne pouvez pas faire d'arithmétique avec eux. Ils ne sont pas compris par le compilateur comme étant équivalents au type étendu.
Par exemple, si :
- Function foo(X:Extended):Extended;
est compilé avec l'ensemble d'options -MC68881 (de sorte que pour cette fonction, le type Extended a une largeur de 96 bits), alors pour appeler foo depuis un monde 80 bits, vous feriez :
- Déclarez foo dans l'interface 80 bits comme suit :
- Function Foo(X:Extended96):Extended96;
- Appelez foo comme :
- X96toX80(foo(X80toX96(X)));