Section courante

A propos

Section administrative du site

Le programme suivant, écrit en Perl, permet le traçage à répétition d'un triangle de «Sierpinski» utilisé dans les fractales. Je me suis permit de mettre à jour un programme inspiré d'une procédure de «Reiner Scholles» écrite à l'origine en Pascal. Avant de commencer assurez-vous d'avoir installé le paquet Tk approprié comme l'exemple suivant :

C:\>ppm install Tk

Voici le code source Perl :

  1. #!/usr/bin/perl
  2.  
  3. use Tk;
  4. use strict;
  5.  
  6. my $Hauteur=25;
  7. my $ValeurFinale=100000;
  8. my (@X,@Y);
  9.  
  10. my $mw = MainWindow->new;
  11. $mw->title("Triangle Sierpinski");
  12. my $canvas = $mw->Canvas( -width=>320, -height=>200, -background=>"black");
  13. $canvas->pack(-expand => 1, -fill => 'both');
  14.  
  15. sub SetPixel($$$) {
  16.  my($x,$y,$color) = @_;
  17.  $canvas->createLine($x, $y, $x + 1, $y + 1, -width => 1, -fill => $color);
  18. }
  19.  
  20. $X[0] = int(320 / 2);
  21. $Y[0] = $Hauteur;
  22. $X[1] = $X[0] - (int(320) - 1) / 3;
  23. $Y[1] = (int(200) - 1) - $Hauteur - 1;
  24. $X[2] = $X[0] + (320 - 1) / 3;
  25. $Y[2] = (200 - 1) - $Hauteur - 1;
  26. my $XP = $X[0];
  27. my $YP = $Y[0];
  28. my $I = 1;
  29.  
  30. sub anim() {
  31.    if($I <= $ValeurFinale) {
  32.      my $P = rand(2 + 1);
  33.      $XP = int(($XP + $X[$P]) / 2);
  34.      $YP = int(($YP + $Y[$P]) / 2);
  35.      SetPixel($XP, $YP, "yellow");
  36.      $I++;
  37.    }
  38. }
  39.  
  40. my $id = $mw->repeat(5, \&anim);
  41.  
  42. MainLoop;

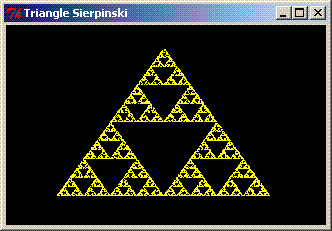
Voici en terminant un exemple du résultat de se petit programme:

Dernière mise à jour : Jeudi, le 17 janvier 2019