Fonctions mathématiques
Cette page traite des mathématiques que le ZX Spectrum peut gérer. Très probablement, vous n'aurez jamais à utiliser tout cela, donc si vous trouvez que c'est trop lourd, n'ayez pas peur de sauter cette page. Il couvre l'opération ↑ (élevant à une puissance), les fonctions EXP et LN et les fonctions trigonométriques SIN, COS, TAN et leurs inverses ASN, ACS et ATN.
↑ et EXP
Vous pouvez élever un nombre à la puissance d'un autre - cela signifie «multiplier le premier nombre par lui-même le deuxième nombre de fois». Ceci est normalement indiqué en écrivant le deuxième chiffre juste au-dessus et à droite du premier chiffre ; mais évidemment, ce serait difficile sur un ordinateur, nous utilisons donc le symbole ↑ à la place. Par exemple, les puissances de 2 sont :
| Formule | Signification |
|---|---|
| 2↑1=2 | 2*1=2 |
| 2↑2=2*2=4 | (2 au carré, normalement écrit 22) |
| 2↑3=2*2*2=8 | (2 au cube, normalement écrit 23) |
| 2↑4=2*2*2*2=16 | (2 à la puissance quatre, normalement écrit 24) |
Ainsi, à son niveau le plus élémentaire, 'a ↑ b' signifie 'a multiplié par lui-même b fois', mais évidemment cela n'a de sens que si b est un nombre entier positif. Pour trouver une définition fonctionnant pour d'autres valeurs de b, nous considérons la règle :
| a ↑ (b+c)=a ↑ b*a ↑ c |
Notez qu'ils donnes ↑ une priorité supérieure à * et / de sorte que lorsqu'il y a plusieurs opérations dans une expression, le ↑ s sont évalués avant les *s et /s.) Vous ne devriez pas avoir besoin d'être convaincu que cela fonctionne lorsque b et c sont tous deux des nombres entiers positifs ; mais si nous décidons que nous voulons que cela fonctionne même quand ils ne le sont pas, alors nous nous retrouvons obligés d'accepter que :
- a↑0=1
- a↑(-b)=1/a ↑ b
- a ↑ (1/b)=la bième racine de a, c'est-à-dire le nombre qu'il faut multiplier par lui-même b fois pour obtenir a
et :
| a ↑ (b*c)=(a ↑ b) ↑ c |
Si vous n'avez jamais rien vu de tout cela auparavant, n'essayez pas de vous en souvenir tout de suite; rappelez-vous juste que :
| a ↑ (-1)=1/a |
et :
| a ↑ (1/2)=SQR a |
et peut-être que lorsque vous serez familiarisé avec ceux-ci, le reste commencera à avoir un sens. Expérimentez avec tout cela en essayant ce programme :
Bien sûr, si la règle que nous avons donnée plus tôt est vraie, alors à chaque fois, les deux nombres affichés par l'ordinateur seront égaux. (Remarque - en raison de la façon dont l'ordinateur calcule ↑, le nombre à gauche - a dans ce cas - ne doit jamais être négatif.)
Un exemple assez typique de ce à quoi cette fonction peut servir est celui des intérêts composés. Supposons que vous gardiez une partie de votre argent dans une société de construction et qu'elle rapporte 15 % d'intérêt par an. Ensuite, après un an, vous n'aurez pas seulement les 100 % que vous aviez de toute façon, mais également les 15 % d'intérêt que la société de construction vous a accordés, soit au total 115 % de ce que vous aviez à l'origine. Pour le dire autrement, vous avez multiplié votre somme d'argent par 1,15, et cela est vrai quel que soit le montant que vous aviez là-bas en premier lieu. Après une autre année, la même chose se sera reproduite, de sorte que vous aurez alors 1,15*1,15=1,15 ↑ 2=1,3225 fois votre somme d'argent initiale. En général, après y ans, vous aurez 1,15 ↑ y fois ce avec quoi vous étiez au départ.
Si vous essayez cette commande :
vous verrez que même en partant de £10, tout monte assez rapidement, et qui plus est, cela devient de plus en plus rapide au fil du temps. (Bien que même ainsi, vous pourriez toujours constater qu'il ne suit pas l'inflation.)
Ce type de comportement, où après un intervalle de temps fixe une quantité se multiplie par une proportion fixe, est appelé croissance exponentielle, et il est calculé en élevant un nombre fixe à la puissance du temps.
Supposons que vous ayez fait ceci :
- 10 DEF FN a(x)=a ↑ x
Ici, a est plus ou moins fixe, par des instructions LET: sa valeur correspondra au taux d'intérêt, ne changeant que de temps en temps.
Il y a une certaine valeur pour a rendant la fonction FN particulièrement jolie à l'oeil averti d'un mathématicien : et cette valeur s'appelle e. Le ZX Spectrum a une fonction appelée EXP définie par :
| EXP x = e ↑ x |
Malheureusement, e lui-même n'est pas un nombre particulièrement joli : c'est une décimale infinie non récurrente. Vous pouvez voir ses premières décimales en faisant :
car EXP 1 = e ↑ 1 = e. Bien sûr, ce n'est qu'une approximation. Vous ne pouvez jamais écrire e exactement.
LN
L'inverse d'une fonction exponentielle est une fonction logarithmique : le logarithme (en base a) d'un nombre x est la puissance à laquelle il faut élever a pour obtenir le nombre x, et cela s'écrit logax. Ainsi par définition un ↑ logax=x ; et il est également vrai que log(a ↑ x)=x.
Vous savez peut-être déjà comment utiliser les logarithmes en base 10 pour effectuer des multiplications ; ceux-ci sont appelés logarithmes communs. Le ZX Spectrum a une fonction LN calculant les logarithmes à la base e ; ceux-ci sont appelés logarithmes naturels. Pour calculer les logarithmes à toute autre base, vous devez diviser le logarithme naturel par le logarithme naturel de la base :
| logax=LN x/LN a |
PI
Étant donné n'importe quel cercle, vous pouvez trouver son périmètre (la distance autour de son bord, souvent appelée sa circonférence) en multipliant son diamètre (largeur) par un nombre appelé π. (π est un p grec, et il est utilisé parce qu'il représente le périmètre. Son nom est pi.)
Comme e, π est un nombre décimal infini non récurrent ; il commence par 3.141592653589... Le mot PI sur le Spectrum (mode étendu, puis M) est considéré comme représentant ce nombre - essayez :
SIN, COS et TAN; ASN, ACS et ATN
Les fonctions trigonométriques mesurent ce qui se passe lorsqu'un point se déplace autour d'un cercle. Voici un cercle de rayon 1 (1 quoi ? Peu importe, tant qu'on garde la même unité tout du long. Rien ne vous empêche d'inventer une nouvelle unité à vous pour chaque cercle que vous traversez intéresser) et un point le contournant. Le point a commencé à la position 3 heures, puis s'est déplacé dans le sens inverse des aiguilles d'une montre.
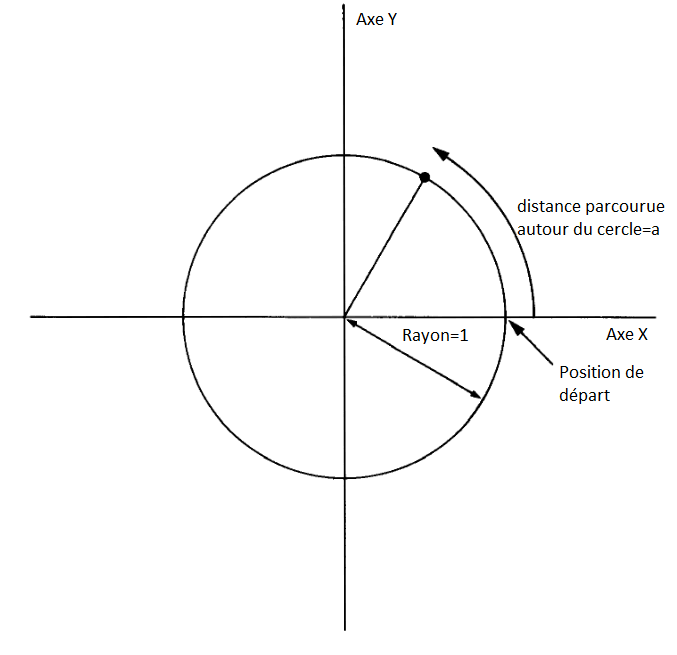
Nous avons également tracé deux lignes appelées axes passant par le centre du cercle. Celui à 9 heures et 3 heures est appelé l'axe des x, et celui à 6 heures et 12 heures est appelé l'axe des y.
Pour spécifier où se trouve le point, vous dites de quelle distance il s'est déplacé autour du cercle depuis sa position de départ à 3 heures : appelons cette distance a. Nous savons que la circonférence du cercle est de 2π (car son rayon est 1 et son diamètre est donc 2) : donc lorsqu'il s'est déplacé d'un quart du tour de cercle, a=π/2; lorsqu'il s'est déplacé à mi-chemin, a = π ; et quand il a fait tout le tour, a=2π.
Étant donné la distance courbée autour du bord, a, deux autres distances que vous aimeriez savoir sont à quelle distance se trouve le point à droite de l'axe des y et à quelle distance il se trouve au-dessus de l'axe des x. Ceux-ci sont appelés, respectivement, le cosinus et le sinus de a. Les fonctions COS et SIN sur l'ordinateur les calculeront.
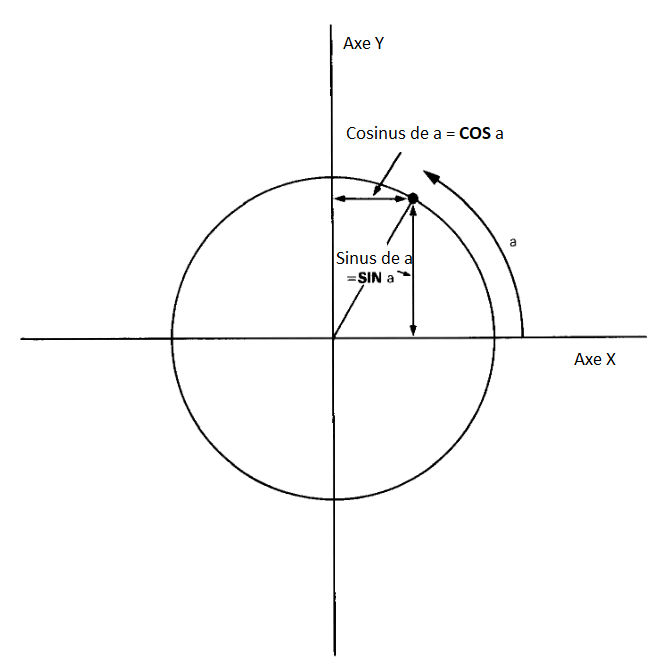
Notez que si le point va à gauche de l'axe y, alors le cosinus devient négatif ; et si le point passe en dessous de l'axe des abscisses, le sinus devient négatif.
Une autre propriété est qu'une fois que a atteint 2π, le point revient à son point de départ et le sinus et le cosinus recommencent à prendre les mêmes valeurs :
La tangente de a est définie comme étant le sinus divisé par le cosinus ; la fonction correspondante sur l'ordinateur est appelée TAN.
Parfois, nous devons travailler ces fonctions en sens inverse, en trouvant la valeur de a ayant donné le sinus, le cosinus ou la tangente. Les fonctions pour ce faire sont appelées arcsine (ASN sur l'ordinateur), arc-cosinus (ACS) et arc-tangente (ATN).
Dans le diagramme du point se déplaçant autour du cercle, regardez le rayon joignant le centre au point. Vous devriez pouvoir voir que la distance que nous avons appelée a, la distance parcourue par le point autour du bord du cercle, est une façon de mesurer l'angle dont le rayon s'est éloigné de l'axe des x. Lorsque a=π2, l'angle est de 90 degrés ; quand a=π l'angle est de 180 degrés; et donc arrondir à quand a=2π, et l'angle est de 360 degrés. Autant oublier les degrés et mesurer l'angle en a seul : on dit alors que l'on mesure l'angle en radians. Ainsi π/2 radians=90 degrés et ainsi de suite.
Vous devez toujours vous rappeler que sur le SIN, COS du ZX Spectrum et ainsi de suite, utilise des radians et non des degrés. Pour convertir des degrés en radians, divisez par 180 et multipliez par π; pour reconvertir des radians en degrés, vous divisez par π et multiplier par 180.



