Introduction

Les arbres sont des structures récursive non-linéaires construit à partir de noeud dont chacun de ces noeuds pointera vers deux autres noeuds avec des branches récursives de façon à contenir toutes les données d'une structure ou d'une liste. Chacun des éléments, aussi appelé noeuds, doivent être du même type et sont reliés à l'aide de pointeur définit par le terme de branche. De cette façon, on comprendra qu'un arbre de type de base T sera soit :

• Une structure vide
• Un noeud de type T (pour la racine) par lequel sera associé un nombre fini de sous-arbres descendants.

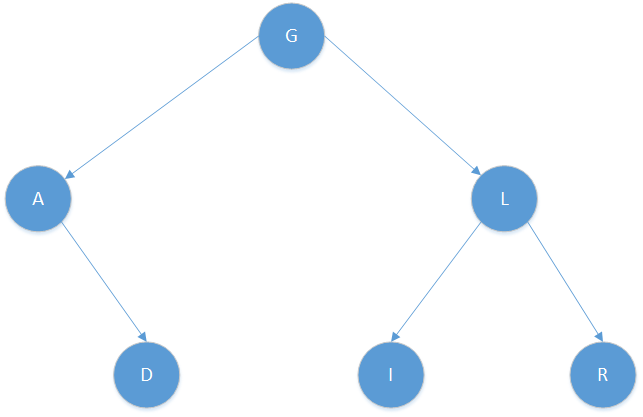
Par conséquent, on obtiendra les notions suivantes :

• Niveau d'un noeud : Le niveau d'un noeud correspond au nombre d'arc qu'il faut traverser afin d'arriver à ce noeud. Aussi, la racine de l'arbre correspond toujours au premier niveau ou au niveau 1.
• Feuille : Les noeuds de terminaison, les noeuds terminaux ou les feuilles représentent des noeuds n'ayant pas de descendant. A l'opposer, les noeuds ayant au moins une branche sont appelées des noeuds non-terminaux ou noeuds intérieurs.
• Hauteur : La hauteur d'un arbre, aussi appelé la profondeur d'un arbre, correspond au nombre d'arcs maximum qu'il faut traverser pour aller de la racine de l'arbre jusqu'à une feuille.
• Descendant : Un noeud situé immédiatement sous un noeud parent, est appelé un noeud descendant directe et l'ancêtre directe.
• Degré de noeud : Le nombre de branches associés à un noeud (nombre de descendant direct) correspond au degré de noeud. Aussi, le degré d'un arbre est égale au degré le plus élevé de ses noeuds. De plus, une liste linéaire est considéré comme un arbre de degré 1.
• Chemin d'un noeud : La suite d'arc menant de la racine à ce noeud est appelé le chemin d'un noeud.
• Arbre binaire : Un arbre de degré 2 est aussi appelé un arbre binaire, tandis que les arbres avec un degré supérieur à 2 sont appelés un arbre multiple.
• Arbre équilibré : On appel, un arbre équilibré, un arbre dont chacune des niveaux de branches ne varie pas d'un niveau à l'autre.
• Arbre ordonné : On appel, un arbre ordonné, un arbre dont la position respective des branches reflètes une relation d'ordre.
• Formule : Le profondeur d'un arbre équilibré peut être obtenir à l'aide de la formule suivante, où N correspond au noeud :

Profondeur	Formule
Minimum	log2(N + 1)
Maximum	√2 x log2(N + 2) -(√5 - 2)

Les arbres binaires ordonnés

On utilise généralement l'arbre binaire ordonné pour des arbres de tri, des arbres syntaxiques, des arbres généalogiques et des branches de versions. Ainsi, ce genre d'arbre permettra d'entreposer des informations avec une forme de hiérarchie entre ses différentes informations. Cette hiérarchie est représenté par des liens de dépendances (branche) entre les différentes données, soit par gauche et par droite. Voici une représentation de la structure de données suivantes en langage de programmation Pascal :