Introduction
L'algorithme du Triangle de Sierpinski est une méthode géométrique récursive pour générer une fractale en forme de triangle. Le principe de cet algorithme est de partir d'un grand triangle équilatéral, puis de diviser ce triangle en quatre sous-triangles équilatéraux plus petits. Le sous-triangle central est ensuite retiré, ce qui crée une première itération de la fractale.
Voici comment fonctionne l'algorithme en étapes :
- Démarrage : On commence avec un grand triangle équilatéral.
- Division récursive : À chaque étape de l'algorithme, chaque triangle restant est divisé en trois sous-triangles équilatéraux en traçant des segments de droite reliant les milieux des côtés du triangle.
- Suppression du centre : Le triangle central obtenu après la division est retiré, créant un motif de trous au sein du grand triangle initial.
- Itération : Le processus est répété récursivement pour chaque sous-triangle. À chaque itération, on obtient un motif de trous de plus en plus petits, formant la structure caractéristique du triangle de Sierpinski.
Le Triangle de Sierpinski est un exemple classique de fractale en raison de sa nature auto-similaire : chaque sous-partie du triangle est une version réduite et semblable du triangle entier. L'algorithme continue théoriquement indéfiniment, mais en pratique, il est souvent limité par un nombre d'itérations déterminé pour des raisons de temps de calcul et de résolution graphique.
Cet algorithme est fréquemment utilisé dans les domaines de l'infographie et des mathématiques pour illustrer des concepts de récursivité et d'auto-similarité.
Algorithme
Voici un algorithme en pseudo-code pour dessiner le Triangle de Sierpinski en utilisant une approche récursive. L'idée est de diviser chaque triangle en trois sous-triangles à chaque itération et de retirer le triangle central. Cet algorithme peut être implémenté graphiquement en utilisant des coordonnées pour dessiner des triangles, ou simplement pour générer une structure récursive.
|
MODULE dessinerTriangleSierpinski(x1, y1, x2, y2, x3, y3, profondeur) SI profondeur = 0 ALORS dessinerTriangle(x1, y1, x2, y2, x3, y3) RETOURNE FIN SI * Calcul des points au milieu de chaque côté du triangle mx1 ← (x1 + x2) / 2 my1 ← (y1 + y2) / 2 mx2 ← (x2 + x3) / 2 my2 ← (y2 + y3) / 2 mx3 ← (x3 + x1) / 2 my3 ← (y3 + y1) / 2 * Appels récursifs pour les trois sous-triangles dessinerTriangleSierpinski(x1, y1, mx1, my1, mx3, my3, profondeur - 1) dessinerTriangleSierpinski(mx1, my1, x2, y2, mx2, my2, profondeur - 1) dessinerTriangleSierpinski(mx3, my3, mx2, my2, x3, y3, profondeur - 1) |
Exemple en langage de programmation GWBASIC
Voici un exemple d'un Triangle de Sierpinski écrit en GWBASIC :
- 10 SCREEN 1
- 20 Hauteur=25
- 30 ValeurFinale=30000
- 40 DIM X(3),Y(3)
- 50 X(0)=INT(320/2)
- 60 Y(0)=Hauteur
- 70 X(1)=X(0)-(INT(320)-1) / 3
- 80 Y(1)=(INT(200)-1)-Hauteur-1
- 90 X(2)=X(0)+(320-1) / 3
- 100 Y(2)=(200-1)-Hauteur-1
- 110 XP=X(0)
- 120 YP=Y(0)
- 130 RANDOMIZE TIMER
- 140 FOR I=1 TO ValeurFinale
- 150 P=INT(RND*3)
- 160 XP=INT((XP+X(P)) / 2)
- 170 YP=INT((YP+Y(P)) / 2)
- 180 PSET(XP,YP)
- 190 NEXT
Voici en terminant un exemple du résultat de se petit programme :

Exemple en langage de programmation Perl
Voici un exemple d'un Triangle de Sierpinski écrit en Perl :
- #!/usr/bin/perl
-
- use Tk;
- use strict;
-
- my $Hauteur=25;
- my $ValeurFinale=100000;
- my (@X,@Y);
-
- my $mw = MainWindow->new;
- $mw->title("Triangle Sierpinski");
- my $canvas = $mw->Canvas( -width=>320, -height=>200, -background=>"black");
- $canvas->pack(-expand => 1, -fill => 'both');
-
- sub SetPixel($$$) {
- my($x,$y,$color) = @_;
- $canvas->createLine($x, $y, $x + 1, $y + 1, -width => 1, -fill => $color);
- }
-
- $X[0] = int(320 / 2);
- $Y[0] = $Hauteur;
- $X[1] = $X[0] - (int(320) - 1) / 3;
- $Y[1] = (int(200) - 1) - $Hauteur - 1;
- $X[2] = $X[0] + (320 - 1) / 3;
- $Y[2] = (200 - 1) - $Hauteur - 1;
- my $XP = $X[0];
- my $YP = $Y[0];
- my $I = 1;
-
- sub anim() {
- if($I <= $ValeurFinale) {
- my $P = rand(2 + 1);
- $XP = int(($XP + $X[$P]) / 2);
- $YP = int(($YP + $Y[$P]) / 2);
- SetPixel($XP, $YP, "yellow");
- $I++;
- }
- }
-
- my $id = $mw->repeat(5, \&anim);
-
- MainLoop;
Voici en terminant un exemple du résultat de se petit programme :
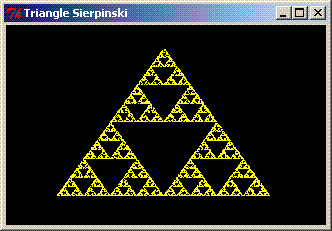
Exemple en langage de programmation PowerBASIC
Voici un exemple d'un Triangle de Sierpinski écrit en PowerBASIC :
- SCREEN 1
- Hauteur=25
- ValeurFinale=30000
- DIM X(3),Y(3)
- X(0)=INT(320/2)
- Y(0)=Hauteur
- X(1)=X(0)-(INT(320)-1) / 3
- Y(1)=(INT(200)-1)-Hauteur-1
- X(2)=X(0)+(320-1) / 3
- Y(2)=(200-1)-Hauteur-1
- XP=X(0)
- YP=Y(0)
- RANDOMIZE TIMER
- FOR I=1 TO ValeurFinale
- P=INT(RND*3)
- XP=INT((XP+X(P)) / 2)
- YP=INT((YP+Y(P)) / 2)
- PSET(XP,YP)
- NEXT
Voici en terminant un exemple du résultat de se petit programme :

Exemple en langage de programmation QuickPascal
Voici un exemple d'un Triangle de Sierpinski écrit en QuickPascal :
- Program TriangleSierpinski;
-
- Uses Crt,MSGraph;
-
- Const
- GetMaxScreenX=320;
- GetMaxScreenY=200;
- Hauteur=25;
- ValeurFinale=30000;
-
- Var
- X,Y:Array[0..2]of Word;
- Err,XP,YP,I,P:Word;
-
- BEGIN
- Err:=_SetVideoMode(_VRes2Color);
- _SetColor(WHITE);
- Randomize;
- X[0]:=GetMaxScreenX shr 1;
- Y[0]:=Hauteur;
- X[1]:=X[0]-(GetMaxScreenX div 3);
- Y[1]:=GetMaxScreenY-Hauteur-1;
- X[2]:=X[0]+(GetMaxScreenX div 3);
- Y[2]:=GetMaxScreenY-Hauteur-1;
- XP:=X[0];YP:=Y[0];
- For I:=1 TO ValeurFinale do Begin
- P:=Random(3);
- XP:=(XP+X[P])shr 1;
- YP:=(YP+Y[P])shr 1;
- _SetPixel(XP,YP);
- End;
- Repeat Until KeyPressed;
- END.
Voici en terminant un exemple du résultat de se petit programme :






