Algorithme à germes
L'algorithme à germes, aussi appelé algorithme de remplissage par diffusion, est un algorithme permettant d'effectuer le remplissage d'une surface de taille et de contours inconnus avec une couleur précise de délimitation. Elle est utilisé par exemple avec l'instruction PAINT de GWBASIC, PAINT de QBASIC, FloodFill de Turbo Pascal, dans les programmes de dessins Bitmap et mêmes dans certains jeux comme le démineur, Puyo Puyo et Lumines.
Du côté de son fonctionnement, l'algorithme à besoin de lire la couleur où il est situé dans son traçage et se diffuse à partir d'un point centrale, d'où il s'étendra vers le nord, l'est, l'ouest et le sud jusqu'à ce qu'une couleur de contour soit rencontré. L'algorithme cherche les pixels à côté en effectuant un appel récursive de lui-même (d'où le nom de germe) jusqu'à ce qu'il couvert toute la surface possible en vérifiant toujours les couleurs ne correspondant pas à la couleur de contour.
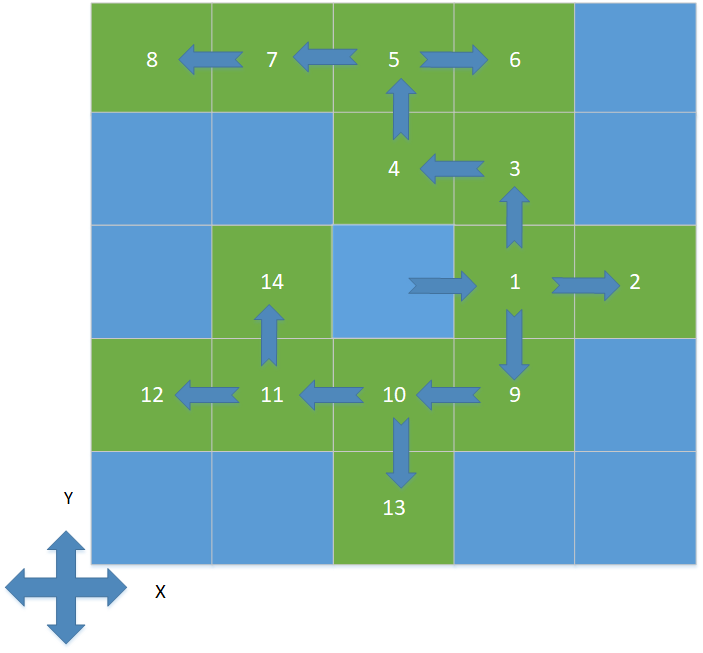
Algorithme
Voici l'algorithme à germes écrit en pseudo-langage, optimiser pour les lignes horizontales, que l'on appel à partir du module FloodFill :
|
NumYPixels ← largeur de l'écran ou de l'image MODULE GetPixel(X,Y) Retourne le pixel (X,Y) ou lit le pixel dans l'image (X,Y) MODULE HorizontalLine(X1,Y,X2) BOUCLE POUR I ← X1 JUSQU'A X2 Affiche pixel (I,Y) ou écrit pixel dans l'image (I,Y) FIN BOUCLE POUR MODULE PredLine(L,R,Y,UpDown) SI GetPixel(L,Y) = C2 ALORS BOUCLE FAIRE TANT QUE (L > 0) ET (GetPixel(L-1,Y) = C2) L ← L - 1 FIN BOUCLE FAIRE TANT QUE FIN SI X ← L SI GetPixel(R,Y) = C2 ALORS BOUCLE FAIRE TANT QUE (R < NumXPixels) ET (GetPixel(R+1,Y) = C2) R ← R + 1 FIN BOUCLE TANT QUE FIN SI BOUCLE FAIRE TANT QUE X ≤ R X2 ← X SI GetPixel(X,Y) = C2 ALORS BOUCLE FAIRE TANT QUE (GetPixel(X+1,Y) = C2) ET (X < NumXPixels) X ← X + 1 FIN BOUCLE TANT QUE * HorizontalLine(X2,Y,X) Affiche pixel(X2,Y) Affiche pixel(X,Y) SI UpDown = 2 ALORS SI Y < 0 ALORS APPEL PredLine(X2,X,Y-1,2) FIN SI SI Y < NumYPixels ALORS SI(L > X2) ET (R < X) ALORS APPEL PredLine(X2,L-1,Y+1,1) APPEL PredLine(R+1,X,Y+1,1) SINON SI (L ≤ X2) ET (R < X) ALORS APPEL PredLine(R+1,X,Y+1,1) SINON SI (L > X2) ET (R ≥ X) ALORS APPEL PredLine(X2,L-1,Y+1,1) FIN SI FIN SI SI UpDown = 1 ALORS SI Y < NumYPixels ALORS APPEL PredLine(X2,X,Y+1,1) SINON SI Y > 0 ALORS SI(L > X2) ET (R < X) ALORS APPEL PredLine(X2,L-1,Y-1,2) APPEL PredLine(R+1,X,Y-1,2) SINON SI(L ≤ X2) ET (R < X) ALORS APPEL PredLine(R+1,X,Y-1,2) SINON SI ( L > X2) ET (R ≥ X) ALORS APPEL PredLine(X2,L-1,Y-1,2) FIN SI FIN SI FIN SI FIN SI X ← X + 1 FIN BOUCLE TANT QUE MODULE FloodFill(X,Y) C2 ← GetPixel(X,Y) APPEL PredLine(X,X,Y,2) APPEL PredLine(X,X,Y+1,1) |
C'est algorithme n'est pas parfaite, ainsi, dans certaines situations, elle peut se retrouver coincé dans une boucle infinie. Dans cette situation, il faudra trouver une façon de l'adapter au contexte réelle soit en lui mettant une limite ou soit faire une sorte qu'il puisse se terminer par une événements clavier par exemple.